TheMaze [source code]
public class TheMaze {
static
/******************************************************************************/
class Solution {
static int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
Set<Integer> set = new HashSet<> ();
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
Queue<int[]> queue = new LinkedList<> ();
for (int[] incre : directions) {
if (!isWall (maze, start[0] + incre[0], start[1] + incre[1]))
queue.offer (new int[] {start[0], start[1], incre[0], incre[1]});
set = new HashSet<> ();
while (!queue.isEmpty ()) {
int size = queue.size ();
for (int i = 0; i < size; i++) {
int[] cur = queue.poll (), direction = new int[] {cur[2], cur[3]};
int x = cur[0], y = cur[1];
if (!set.add (key (x, y, direction)))
continue;
if (x == destination[0] && y == destination[1]) {
if (isWall (maze, x + direction[0], y + direction[1]))
return true;
}
if (isWall (maze, x + direction[0], y + direction[1])) {
for (int[] increment : directions) {
if (!isWall (maze, x + increment[0], y + increment[1]))
queue.offer (new int[] {x + increment[0], y + increment[1], increment[0], increment[1]});
}
} else if (!isWall (maze, x + direction[0], y + direction[1])) {
queue.offer (new int[] {x + direction[0], y + direction[1], direction[0], direction[1]});
}
}
}
}
return false;
}
int key (int x, int y, int[] direction) {
return x * 100_00_00 + y * 100_00 + direction[0] * 100 + direction[1];
}
boolean isWall (int[][] maze, int x, int y) {
return x < 0 || y < 0 || x >= maze.length || y >= maze[0].length || maze[x][y] == 1;
}
}
/******************************************************************************/
public static void main(String[] args) {
TheMaze.Solution tester = new TheMaze.Solution();
int[][][] inputs = {
{{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}}, {{0,4}, {4,4}}, {{1}},
{{0,0,1,0,0},{0,0,0,0,0},{0,0,0,1,0},{1,1,0,1,1},{0,0,0,0,0}}, {{0,4}, {3,2}}, {{0}},
{{0,0,0,0,1,0,0},{0,0,1,0,0,0,0},{0,0,0,0,0,0,0},{0,0,0,0,0,0,1},{0,1,0,0,0,0,0},{0,0,0,1,0,0,0},{0,0,0,0,0,0,0},{0,0,1,0,0,0,1},{0,0,0,0,1,0,0}}, {{0,0}, {8,6}}, {{1}},
};
for (int i = 0; i < inputs.length / 3; i++) {
int[][] maze = inputs[3 * i];
int[] start = inputs[3 * i + 1][0], destination = inputs[3 * i + 1][1];
boolean ans = inputs[3 * i + 2][0][0] == 1;
System.out.println (Printer.separator ());
boolean output = tester.hasPath (maze, start, destination);
System.out.printf ("%s\n and [%s] and [%s] -> %s, expected: %b\n",
Matrix.printMatrix (maze), Printer.array (start), Printer.array (destination), Printer.wrapColor (output + "", output == ans ? "green" : "red"), ans
);
}
}
}
leaf vs. pre-leaf
以前经常讨论leaf判断和pre-leaf判断的区别; 这个不仅仅是一个比如tree结构里面的概念, 就是比较普通的分段算法, 其实也有这个概念, 比如是自己等待一个switch的后半段(比如1->0的0), 还是在1的时候, 就提前peek neighbor. 我个人一般倾向于前一种做法, 因为我认为前一种做法可以降低access数量; 但是实际上, 在考虑语言的优化的情况下, 这个优势并不一定明显, 因为有很多各种cache, 而我这里的这些重复access其实又是有高度的locality的;
另外一个问题需要注意的就是, pre-leaf的思路很多时候可以让问题好写很多;
这题比如, 有一个event, 就是撞墙然后切换direction; 这个就不好用leaf来写, 因为等到你走到1的时候再发现自己之前不应该走到这里, 这个就比较姜了;
这个题目写的时候发现难点在于怎么决定terminate; 一开始的一个想法是用普通的visited这种东西来flag; 但是后来发现这种做法很naive, 因为这个问题其实是允许在一次DFS的过程当中多次走过一个entry的;
后来想过一个方法, 在recurse的时候, 假如撞墙了, 然后马上准备选择下一个方向, 那么要决定下一个选择的方向不能是刚才来的时候的方向的正好相反的方向; 写完这个的时候还认为挺正确的, 完美的解决了一个DFS当中回头的问题; 但是实际上这个思路并不正确, 虽然这个思路避免了一条直线上的来回往复, 但是没哟避免一个cycle, 也就是比如题目描述里面给的这个例子里面, 左上角的这个小空间里面, 可能会有有一个cycle这样的不停的重复;
后来想了想只能用set来解决了;
最后其实写出来一个大概能跑的思路, 但是这个题目比较恶心的地方是故意用大case爆栈, 最后把我这个算法给break掉了, 代码如下:
class Solution {
static int[][] directions = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
Set<Integer> set = new HashSet<> ();
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
boolean res = false;
for (int[] direction : directions)
if (!isWall (maze, start[0] + direction[0], start[1] + direction[1])) {
set = new HashSet<> ();
res = res || dfs (maze, start[0], start[1], destination, direction);
}
return res;
}
boolean dfs (int[][] maze, int x, int y, int[] destination, int[] direction) {
if (set.contains (key (x, y, direction)))
return false; // why FALSE here?
set.add (key (x, y, direction));
if (x == destination[0] && y == destination[1]) {
if (isWall (maze, x + direction[0], y + direction[1]))
return true;
}
boolean res = false;
if (isWall (maze, x + direction[0], y + direction[1])) {
for (int[] increment : directions) {
if (increment[0] == -direction[0] && increment[1] == -direction[1])
continue;
if (!isWall (maze, x + increment[0], y + increment[1]))
res = res || dfs (maze, x + increment[0], y + increment[1], destination, increment);
}
} else if (!isWall (maze, x + direction[0], y + direction[1])) {
res = dfs (maze, x + direction[0], y + direction[1], destination, direction);
}
return res;
}
int key (int x, int y, int[] direction) {
return x * 100_00_00 + y * 100_00 + direction[0] * 100 + direction[1];
}
boolean isWall (int[][] maze, int x, int y) {
return x < 0 || y < 0 || x >= maze.length || y >= maze[0].length || maze[x][y] == 1;
}
}
因为只要当input大到一定程度, recursion就hold不住了; 尽管如此, 这个题目其实还是让我学到了很多东西的;
collection hash and class hash
最后决定用hash来去重, 刚开始的时候我还自己定义了一个类似{int, int int[]}的class, 但是最后发现这个class无法完成去重, 后来想了一下, 是自然的, 这个自己定义的class, 不同的object之间, 就算是member field都相同, 最后JVM给的hash其实也是不同的, 这个也是我们希望的结果;
collection hash and array hash
下一个方案自然而然的就是想要用array, 但是结果发现, array的hash居然也不行!!! 很奇怪, 还特意在REPL上面玩了一下, 真的是这样, array的hash也不是unique to the contents的;
最后只能自己干脆用integer hash来做了, 不过上面的教训还是要了解一下;
对于DFS visited的新理解: augmented
另外, 自己其实已经长时间习惯了DFS问题当中直接一个visited就能够解决, 但是实际上那个只是对于坐标的一个去重. 如果像这里这样, 还想要保证方向的一致性, 那么就要用更加加强型的办法, 比如这里的自己用set来做; hash最终看来, 还是去重的终极办法;
最后, 自己改成BFS之后, 成功AC了, 虽然速度有点丢人: 60ms (3%), 估计应该有更好的方法;
在写这个方法的时候, 一个小的细节就是, 你的set, 要从root出发的每一次BFS都要Reset: 不同的BFS之间不能公用一个set; 这个是一个稍微有点subtle的点;
editorial
Approach #1 Depth First Search [Time Limit Exceeded]
public class Solution {
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
boolean[][] visited = new boolean[maze.length][maze[0].length];
return dfs(maze, start, destination, visited);
}
public boolean dfs(int[][] maze, int[] start, int[] destination, boolean[][] visited) {
if (visited[start[0]][start[1]])
return false;
if (start[0] == destination[0] && start[1] == destination[1])
return true;
visited[start[0]][start[1]] = true;
int r = start[1] + 1, l = start[1] - 1, u = start[0] - 1, d = start[0] + 1;
while (r < maze[0].length && maze[start[0]][r] == 0) // right
r++;
if (dfs(maze, new int[] {start[0], r - 1}, destination, visited))
return true;
while (l >= 0 && maze[start[0]][l] == 0) //left
l--;
if (dfs(maze, new int[] {start[0], l + 1}, destination, visited))
return true;
while (u >= 0 && maze[u][start[1]] == 0) //up
u--;
if (dfs(maze, new int[] {u + 1, start[1]}, destination, visited))
return true;
while (d < maze.length && maze[d][start[1]] == 0) //down
d++;
if (dfs(maze, new int[] {d - 1, start[1]}, destination, visited))
return true;
return false;
}
}
他这个算法就写的很手动; 在每一个位置直接先走到不能走为止, 然后再DFS; 不过其实我感觉跟我的做法最后没有太大的差别, 因为他就算是在当前的iteration一口气走到头了, 然后他下一个iteration又是四个方向全都重新开始DFS, 所以最后还是回头了;
不过这个差别还是警惕了一下我的一个常见毛病, 就是经常追求过于generic.
而且他这个算法有一个好处, 可以直接利用我们熟悉的visited来去重, 而不需要手动的augment; 为什么他这个可以这样做?
我后来想了一下, 大概是这个原因, 虽然说他用的这个flag和我用的都叫一样的名字, 都叫visited, 但是我们对其的定义的内涵不一样的; 我的定义的就真的只是"经过"而已, 而他的这个定义的, 严格来说应该叫做started. 所以他这个可以直接用这个flag来严格限制每一个entry只发生一次. 我自己的这种一次只走一步的方法, 则不能, 最后会导致有些实际上可以走的path被我给prune掉了;
Approach #2 Breadth First Search [Accepted]
public class Solution {
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
boolean[][] visited = new boolean[maze.length][maze[0].length];
int[][] dirs={{0, 1}, {0, -1}, {-1, 0}, {1, 0}};
Queue < int[] > queue = new LinkedList < > ();
queue.add(start);
visited[start[0]][start[1]] = true;
while (!queue.isEmpty()) {
int[] s = queue.remove();
if (s[0] == destination[0] && s[1] == destination[1])
return true;
for (int[] dir: dirs) {
int x = s[0] + dir[0];
int y = s[1] + dir[1];
while (x >= 0 && y >= 0 && x < maze.length && y < maze[0].length && maze[x][y] == 0) {
x += dir[0];
y += dir[1];
}
if (!visited[x - dir[0]][y - dir[1]]) {
queue.add(new int[] {x - dir[0], y - dir[1]});
visited[x - dir[0]][y - dir[1]] = true;
}
}
}
return false;
}
}
他这个依然是用一口气走完的思路写的一个BFS, 但是最后的速度比我的写法快很多; 注意怎样在BFS当中apply visited这样的pruning, 以前好像还没怎么见到过;
另外注意他这种一口气的写法, 还有一个优势就是最后成功条件的判断更简单: 他这个只要最后能够碰到终点, 就肯定是正确的, 而不用像我的做法那样, 还要先判断说, 虽然我们现在站在终点了, 但是前方要无路可走; 从这个角度来看, 他这种一口气的做法应该说是更聪明一些的;
在底下的评论里面, 有另外一个recursion的DFS, 居然被AC了:
// dfs solution
class Solution {
private int[] dr;
private int[] dc;
private int[][] MAZE;
private int R;
private int C;
private int[] dest;
private boolean res;
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
dr = new int[]{-1, 1, 0, 0}; // u d l r
dc = new int[]{0, 0, -1, 1}; // u d l r
MAZE = maze;
R = maze.length;
C = maze[0].length;
dest = destination;
res = false;
// doesn't care the initial direction parameter
dfs(-1, start, new boolean[R][C]);
return res;
}
private void dfs(int dir, int[] start, boolean[][] visited) {
int r = start[0], c = start[1];
if (Arrays.equals(start, dest)) {
res = true;
return;
}
if (visited[r][c]) return;
visited[r][c] = true;
// up down left right
for (int i = 0; i < 4; ++i) {
if (i == dir) continue; // skip the direction that will hit the wall again
int x = r, y = c;
while (isValid(new int[]{x + dr[i], y + dc[i]})) {
x += dr[i];
y += dc[i];
}
dfs(i, new int[]{x, y}, visited);
}
}
// return true if the coord is valid and maze[coord] == 0;
private boolean isValid(int[] coord) {
int r = coord[0];
int c = coord[1];
if (r < 0 || r >= R || c < 0 || c >= C) return false;
if (MAZE[r][c] == 1) return false;
return true;
}
}
最后速度居然也不错;
另外这个人的代码写的也挺干净的;
思路还是那个一口气的做法, 不过写的稍微简练一些; 与我在traverse的过程中保留increment不同, 他只维护一个index, 虽然本质上应该是差不多的;
discussion一个还是用recursion的解法, 速度倒是很快: 11(86):
public class Solution {
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
// dfs
if (maze == null || start == null || destination == null) {
return false;
}
boolean[][] visited = new boolean[maze.length][maze[0].length];
return hasPath(maze, start, destination, visited);
}
private boolean hasPath(int[][] maze, int[] start, int[] dest, boolean[][] visited) {
int y = start[0];
int x = start[1];
if (visited[y][x]) return false;
visited[y][x] = true;
if (x == dest[1] && y == dest[0]) {
return true;
}
// left
if (x > 0 && maze[y][x-1] != 1) {
int i = x - 1;
while (i > 0 && maze[y][i-1] != 1) i--;
if (hasPath(maze, new int[]{y, i}, dest, visited)) return true;
}
//right
if (x < maze[0].length - 1 && maze[y][x+1] != 1) {
int i = x + 1;
while (i < maze[0].length-1 && maze[y][i+1] != 1) i++;
if (hasPath(maze, new int[]{y, i}, dest, visited)) return true;
}
//up
if (y > 0 && maze[y-1][x] != 1) {
int i = y - 1;
while (i > 0 && maze[i-1][x] != 1) i--;
if (hasPath(maze, new int[]{i, x}, dest, visited)) return true;
}
//down
if (y < maze.length - 1 && maze[y+1][x] != 1) {
int i = y + 1;
while (i < maze.length-1 && maze[i+1][x] != 1) i++;
if (hasPath(maze, new int[]{i, x}, dest, visited)) return true;
}
return false;
}
}
为什么这个比上面那个DFS快那么多? 感觉都差不多啊; 另外, 事实证明, 只要用的是一口气模式, 实际上是不要维护direction的?
我在上面那个comment解法里面试了一下, 果然真的不需要if (i == dir) continue;这一行; 而且删了之后, 速度根本没有改变; 这个也是符合我之前的分析的; 一口气模式是这个visited简单去重的必要条件; 一个flag不是你想让他代表什么他就代表什么的, 自己脑子里要想清楚, 然后才知道为什么可以直接用一个boolean flag来prune而不会导致出问题;
当然, 为了让去重可以更简单, 可以用这样的single flag, 对于iteration代码的写法也有一个启发就是, do as much work as possible, 这样才可以让你心安理得的不用回头. 而我自己的这个算法, 因为一个iteration只走一步, 完成的工作量很少, 所以就要频繁回头, visited的实现也就复杂很多;
discussion最优解:
public class Solution {
class Point {
int x,y;
public Point(int _x, int _y) {x=_x;y=_y;}
}
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
int m=maze.length, n=maze[0].length;
if (start[0]==destination[0] && start[1]==destination[1]) return true;
int[][] dir=new int[][] {{-1,0},{0,1},{1,0},{0,-1}};
boolean[][] visited=new boolean[m][n];
LinkedList<Point> list=new LinkedList<>();
visited[start[0]][start[1]]=true;
list.offer(new Point(start[0], start[1]));
while (!list.isEmpty()) {
Point p=list.poll();
int x=p.x, y=p.y;
for (int i=0;i<4;i++) {
int xx=x, yy=y;
while (xx>=0 && xx<m && yy>=0 && yy<n && maze[xx][yy]==0) {
xx+=dir[i][0];
yy+=dir[i][1];
}
xx-=dir[i][0];
yy-=dir[i][1];
if (visited[xx][yy]) continue;
visited[xx][yy]=true;
if (xx==destination[0] && yy==destination[1]) return true;
list.offer(new Point(xx, yy));
}
}
return false;
}
}
这个人提出了一个很贱瑞的问题:
@mingzhou1987 said in Easy-understanding Java bfs solution.:
Hi,
May I know why visited update is not inside while loop function when rolling in same direction?
事实上, 我还真的没有想到这一点; 当然, 知道这个问题之后, 答案本身其实是很自然的;
@ckcz123 said in Easy-understanding Java bfs solution.:
@mingzhou1987 There may be a
cross, so we cannot update while rolling.--->--- | | ^ v | | ^ v | | ---<---+--<--- o v |
这个也解决了我写自己的算法的时候的repeated visit的问题; 所以我还是这个观点, 这种一口气做法下的flag grid, 最好还是叫做started, 毕竟visit的意思还是太宽泛了;
另外注意他这个BFS的写法, 他不需要像我那样走四个BFS, 而是直接只看点: 他的每一个iteration只有一个坐标的概念matters, 而不用还要考虑相同的坐标, 但是不同的方向, 对应的是不同的iteration;
这样就导致循环写起来简单很多, 方向的东西, 在操作queue的时候根本不用操心, 只有当你确实需要处理一个坐标的时候, 才去关心到底走什么方向;
这个就是一个对flag进行了合理的命名的做法:
public class Solution {
private static final int[] DIRECTIONS = { 0, 1, 0, -1, 0 };
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
boolean[][] startedHere = new boolean[maze.length][maze[0].length];
return dfs(maze, startedHere, start, destination);
}
private boolean dfs(int[][] maze, boolean[][] startedHere, int[] start, int[] destination) {
if (startedHere[start[0]][start[1]]) return false;
if (Arrays.equals(start, destination)) return true;
startedHere[start[0]][start[1]] = true;
for (int i = 0; i < DIRECTIONS.length - 1; i++) {
int[] newStart = roll(maze, start[0], start[1], DIRECTIONS[i], DIRECTIONS[i + 1]);
if (dfs(maze, startedHere, newStart, destination)) return true;
}
return false;
}
private int[] roll(int[][] maze, int row, int col, int rowInc, int colInc) {
while (canRoll(maze, row + rowInc, col + colInc)) {
row += rowInc;
col += colInc;
}
return new int[]{row, col};
}
private boolean canRoll(int[][] maze, int row, int col) {
if (row >= maze.length || row < 0 || col >= maze[0].length || col < 0) return false;
return maze[row][col] != 1; // 1 is a wall
}
}
其他地方都是类似的;
好像这个maze问题还有不少, 我感觉跟普通的DFS问题的一个区别就是, do as much as possible这个一口气的思路; 希望后面要记住这个差别;
submission最优解: 8(99):
class Solution {
private boolean result = false;
public boolean hasPath(int[][] maze, int[] start, int[] destination) {
dfs(maze, start[0], start[1], destination);
return result;
}
private void dfs(int[][] maze, int curR, int curC, int[] destination) {
if (result == true) return;
if (curR == destination[0] && curC == destination[1]) {
result = true;
return;
}
if (maze[curR][curC] == 2) {
return;
}
maze[curR][curC] = 2;
int r = curR;
int c = curC;
while ((c - 1) >= 0 && maze[r][c - 1] != 1) {
c--;
}
dfs(maze, r, c, destination);
r = curR;
c = curC;
while ((c + 1) < maze[0].length && maze[r][c + 1] != 1) {
c++;
}
dfs(maze, r, c, destination);
r = curR;
c = curC;
while ((r + 1) < maze.length && maze[r + 1][c] != 1) {
r++;
}
dfs(maze, r, c, destination);
r = curR;
c = curC;
while ((r - 1) >= 0 && maze[r - 1][c] != 1) {
r--;
}
dfs(maze, r, c, destination);
}
}
就是加了一些小优化, 总体思路跟上面见过的一个算法是类似的;
注意他这里的visited放到了InPlace的做法; 对应的, 你看他roll的时候判断的是!= 1, 也就是说无论是0(可以通行)还是2(已经处理过了)都可以被其他的iteration继续roll, 这个也是符合上面的一个comment的看法的;
另外一个技巧也是我见过的, 就是一个global switch pruning, 用一个global变量来记录结果, 然后可以prune掉找到我唯一想要的一个结果之后的多于的iteration; 小的提速技巧, 应该是熟悉的;
Problem Description
There is a ball in a maze with empty spaces and walls. The ball can go through empty spaces by rolling up, down, left or right, but it won't stop rolling until hitting a wall. When the ball stops, it could choose the next direction.
Given the ball's start position, the destination and the maze, determine whether the ball could stop at the destination.
The maze is represented by a binary 2D array. 1 means the wall and 0 means the empty space. You may assume that the borders of the maze are all walls. The start and destination coordinates are represented by row and column indexes.
Example 1
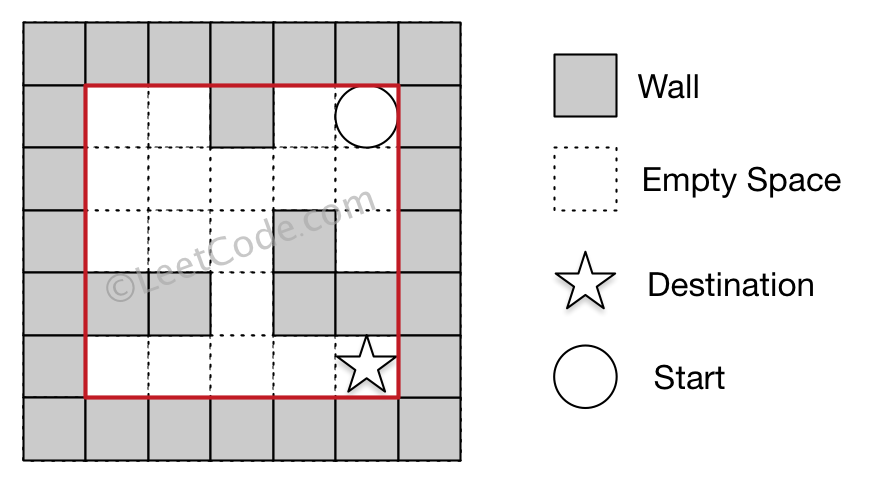
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (4, 4)
Output: true
Explanation: One possible way is : left -> down -> left -> down -> right -> down -> right.
Example 2
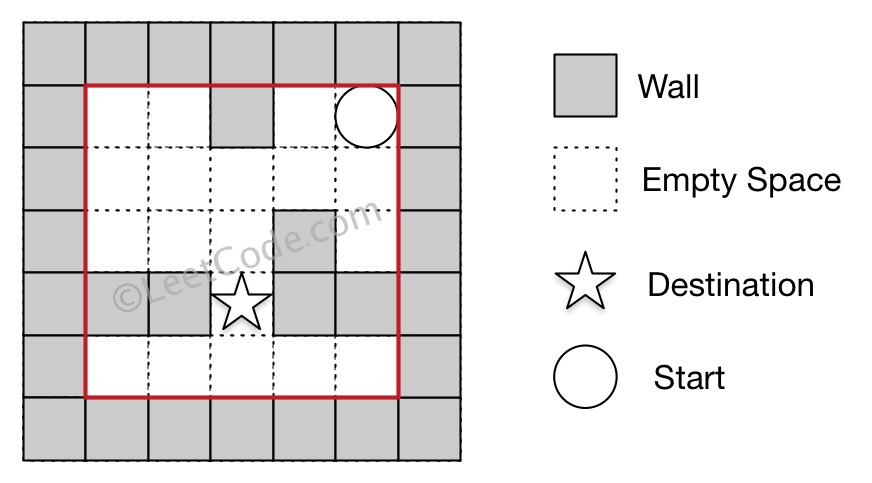
Input 1: a maze represented by a 2D array
0 0 1 0 0
0 0 0 0 0
0 0 0 1 0
1 1 0 1 1
0 0 0 0 0
Input 2: start coordinate (rowStart, colStart) = (0, 4)
Input 3: destination coordinate (rowDest, colDest) = (3, 2)
Output: false
Explanation: There is no way for the ball to stop at the destination.
Note:
- There is only one ball and one destination in the maze.
- Both the ball and the destination exist on an empty space, and they will not be at the same position initially.
- The given maze does not contain border (like the red rectangle in the example pictures), but you could assume the border of the maze are all walls.
- The maze contains at least 2 empty spaces, and both the width and height of the maze won't exceed 100.
Difficulty:Medium
Total Accepted:11K
Total Submissions:25.2K
Contributor:fallcreek
Companies
google
Related Topics
depth-first searchbreadth-first search
Similar Questions
The Maze IIIThe Maze II