CandyCrush [source code]
public class CandyCrush {
static
/******************************************************************************/
class Solution {
public int[][] candyCrush(int[][] board) {
while (crush (board))
drop (board);
return board;
}
/* Inspired by LC 283. Move Zeroes */
void drop (int[][] board) {
int M = board.length, N = board[0].length;
for (int j = 0; j < N; j++) {
int write = M - 1, read = M - 1;
while (read >= 0) {
if (board[read][j] != 0)
board[write--][j] = board[read][j];
read--;
}
for (int i = write; i >= 0; i--)
board[i][j] = 0;
}
}
/* Crush the board by performing three steps.
Return TRUE if any crushing is done at all, indicating that we need to perform a drop after this */
boolean crush (int[][] board) {
boolean res = false;
// Negative flag all to-be-crushed candies in two directions: horizontally and vertically
for (int i = 0; i < board.length; i++) {
int anchor = 0, val = board[i][0];
int j = 0;
for (; j < board[0].length; j++) {
if (board[i][j] != val && board[i][j] != -val) {
if (val != 0 && j - anchor >= 3) {
res = true;
for (int k = anchor; k < j; k++) {
board[i][k] = -Math.abs(board[i][k]);
}
}
anchor = j;
val = board[i][anchor];
}
}
if (val != 0 && j - anchor >= 3) {
res = true;
for (int k = anchor; k < j; k++) {
board[i][k] = -Math.abs(board[i][k]);
}
}
}
for (int j = 0; j < board[0].length; j++) {
int anchor = 0, val = board[0][j];
int i = 0;
for (; i < board.length; i++) {
if (board[i][j] != val && board[i][j] != -val) {
if (val != 0 && i - anchor >= 3) {
res = true;
for (int k = anchor; k < i; k++) {
board[k][j] = -Math.abs(board[k][j]);
}
}
anchor = i;
val = board[anchor][j];
}
}
if (val != 0 && i - anchor >= 3) {
res = true;
for (int k = anchor; k < i; k++) {
board[k][j] = -Math.abs(board[k][j]);
}
}
}
// Clear all negative candies to 0: this is NOT strictly needed.
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] < 0)
board[i][j] = 0;
}
}
return res;
}
}
/******************************************************************************/
public static void main(String[] args) {
CandyCrush.Solution tester = new CandyCrush.Solution();
int[][][] inputs = {
{{110,5,112,113,114},{210,211,5,213,214},{310,311,3,313,314},{410,411,412,5,414},{5,1,512,3,3},{610,4,1,613,614},{710,1,2,713,714},{810,1,2,1,1},{1,1,2,2,2},{4,1,4,4,1014}} ,
{{0,0,0,0,0},{0,0,0,0,0},{0,0,0,0,0},{110,0,0,0,114},{210,0,0,0,214},{310,0,0,113,314},{410,0,0,213,414},{610,211,112,313,614},{710,311,412,613,714},{810,411,512,713,1014}}, //1
};
for (int i = 0; i < inputs.length / 2; i++) {
int[][] board = inputs[2 * i];
System.out.println (Printer.separator ());
String inputStr = Matrix.printMatrix (board);
String outputStr = Matrix.printMatrix (tester.candyCrush (board));
String ansStr = Matrix.printMatrix (inputs[2 * i + 1]);
System.out.printf ("%s ->\n%s, expected:\n%s\n",
inputStr, Printer.wrapColor (outputStr, outputStr.equals (ansStr) ? "green" : "red"), ansStr
);
}
}
}
题目看起来很简单, 但是实际上背后的算法很多细节需要好好考虑;
这题的难点我感觉应该是crush这个过程怎么有效的进行; 感觉直接就crush到0好像不太好; 尝试性的用一个indirecting state的思路来写一下: 加一个中间过程, 以防止太快清零导致其他的crush过程无法查询原有的信息;
好像不行, 想想还是尝试用DFS来做; 毕竟这个题目有一个很明显的connected component的东西在里面;
写的差不多之后突然发现connected component这个思路好像不对; 这个是当时的代码:
class Solution {
static int[][] increments = {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
public int[][] candyCrush(int[][] board) {
return board;
}
void crush (int[][] board) {
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[0].length; j++) {
if (board[i][j] == 0)
continue;
List<int[]> coordinates = new ArrayList<> ();
int[] lrbt = {Integer.MAX_VALUE, Integer.MIN_VALUE, Integer.MAX_VALUE, Integer.MIN_VALUE};
dfs (board, i, j, board[i][j], coordinates, lrbt);
if (lrbt[1] - lrbt[0] >= 2 || lrbt[3] - lrbt[2] >= 2) {
assert coordinates.size () >= 3;
for (int[] coordinate : coordinates)
board[coordinate[0]][coordinate[1]] = 0;
}
}
}
}
void dfs (int[][] board, int x, int y, int key, List<int[]> coordinates, int[] lrbt) {
if (x < 0 || y < 0 || x >= board.length || y >= board[0].length || board[x][y] != key)
return;
coordinates.add (new int[]{x, y});
board[x][y] = -board[x][y];
lrbt[0] = Math.min (lrbt[0], x);
lrbt[1] = Math.max (lrbt[1], x);
lrbt[2] = Math.min (lrbt[2], y);
lrbt[3] = Math.max (lrbt[3], y);
for (int[] increment : increments)
dfs (board, x + increment[0], y + increment[1], key, coordinates, lrbt);
board[x][y] = -board[x][y];
}
}
但是对于题目给的这个例子, crush一次之后就已经发现了问题, 得到的matrix是:
110 5 112 113 114
210 211 5 213 214
310 311 3 313 314
410 411 412 5 414
5 1 512 3 3
610 4 1 613 614
710 0 0 713 714
810 0 0 1 1
0 0 0 0 0
4 0 4 4 1014
跟题目给的结果一对比你就知道哪里有问题了: 单纯的判断connected component的左右和上下长度并不足以决定是否可以清零, 更进一步的, 感觉这个例子也反应出来了这个算法思路本质上的缺陷;
想了想好像还是用indirecting flag的方法可能游戏? 尝试一下;
最后用这个方法还是成功解决了这个问题; crush完成之后, drop本身其实也不难写, 不过这个问题本身还是有难度的, 因为这里这个drop并不是一个非常trivial的算法, 你有没有发现, 这个drop其实就是以前做过的另外一道题目的要求, 就是move 0 to the end of an array那个题目; 这里就应该用这个算法来做; 所以说这个题目真的还是挺难的, 两个步骤都需要一定的思考程度; 最后这个题目也是花了不少的时间, 最后速度是18ms (73%), 可以接受;
整个写完了之后才想起来看一下hint, 果然就是我这里这个思路;
虽然这个题目最后花了很多的时间, 但是不得不说还是学到了很多的东西的; 尤其是对于crush的思考, 走了弯路, 反而也对正确的做法印象更加深刻;
分段算法小结
另外这题的crush步骤里面应用到了分段算法, 这里稍微总结一下我对于分段算法常见的手法
- constant update
- 这个就是discussion里面看到很多人喜欢的一种思路, 就是在run的过程中不停的update类似run_length这样的东西;
- switched update
- 这个是我自己更熟悉的一个思路, 为了保险, 通常需要考虑收尾问题; 细分下面又有两种做法:
- update len: 这个是我本来自己最熟悉的一种做法; 不过这种做法相对更麻烦一些, 因为要频繁的在1based的len和0based的各种index之间进行切换计算;
- update anchor: 这个是看awice大神的解答学到的一种思路, 这种思路的优势在于, 在处理分段的过程当中, anchor本身也是0based的index, 所以最后整个计算非常方便, 只有在最后switch triggerring的时候, 才需要计算判断一下length概念, 这个就相对好处理很多;
- 这个是我自己更熟悉的一个思路, 为了保险, 通常需要考虑收尾问题; 细分下面又有两种做法:
另外一个小的总结, 这题在思考crush的时候, 感觉很overwhelming, 因为感觉有太多的uncertainty: 这个问题我们已经见过很多次了, 看到uncertainty的时候, 不要紧张, 如果实在是没有办法从宏观上面看到什么特别好的解决办法, 那么大不了就enumerate. 毕竟这个是一个题目, 往往在枚举的过程中是可以看到一定的规律的; 就算看不到规律, 总结不出来东西, 好歹对题目思路多少会有一点帮助了;
Editorial
这个是awice大神给出的答案, 非常的有启发性, 跟我的思路也是一致的;
Algorithm
Crushing Step
When crushing, one difficulty is that we might accidentally crush candy that is part of another row. For example, if the board is:
123
145
111
and we crush the vertical row of 1s early, we may not see there was also a horizontal row.
To remedy this, we should flag candy that should be crushed first. We could use an auxillary toCrush boolean array, or we could mark it directly on the board by making the entry negative (ie. board[i][j] = -Math.abs(board[i][j]))
As for how to scan the board, we have two approaches. Let's call a line any row or column of the board.
For each line, we could use a sliding window (or itertools.groupby in Python) to find contiguous segments of the same character. If any of these segments have length 3 or more, we should flag them.
Alternatively, for each line, we could look at each width-3 slice of the line: if they are all the same, then we should flag those 3.
After, we can crush the candy by setting all flagged board cells to zero.
Gravity Step
For each column, we want all the candy to go to the bottom. One way is to iterate through and keep a stack of the (uncrushed) candy, popping and setting as we iterate through the column in reverse order.
Alternatively, we could use a sliding window approach, maintaining a read and write head. As the read head iterates through the column in reverse order, when the read head sees candy, the write head will write it down and move one place. Then, the write head will write zeroes to the remainder of the column.
We showcase the simplest approaches to these steps in the solutions below.
class Solution {
public int[][] candyCrush(int[][] board) {
int R = board.length, C = board[0].length;
boolean todo = false;
for (int r = 0; r < R; ++r) {
for (int c = 0; c + 2 < C; ++c) {
int v = Math.abs(board[r][c]);
if (v != 0 && v == Math.abs(board[r][c+1]) && v == Math.abs(board[r][c+2])) {
board[r][c] = board[r][c+1] = board[r][c+2] = -v;
todo = true;
}
}
}
for (int r = 0; r + 2 < R; ++r) {
for (int c = 0; c < C; ++c) {
int v = Math.abs(board[r][c]);
if (v != 0 && v == Math.abs(board[r+1][c]) && v == Math.abs(board[r+2][c])) {
board[r][c] = board[r+1][c] = board[r+2][c] = -v;
todo = true;
}
}
}
for (int c = 0; c < C; ++c) {
int wr = R - 1;
for (int r = R-1; r >= 0; --r)
if (board[r][c] > 0)
board[wr--][c] = board[r][c];
while (wr >= 0)
board[wr--][c] = 0;
}
return todo ? candyCrush(board) : board;
}
}
整体代码思路是非常类似的, 不过他写的很整洁, 所以最后只需要我的代码一般的长度; 注意他这里一个小技巧, 在crush横竖两个方向的negative mark完成之后, 他没有像我那样加一步清零, 而是直接开始drop, 而在这个drop的move zero的过程当中, 只要判断negative而不是0就行了; 这个是一个我没有想到的小技巧;
另外他认为这个算法复杂度是O((R*C)^2): 一个iteration是RC这个是没有疑问的, 但是WorstCase, 我们一个iteration可能只处理三个candy, 那么最后iteration数量就又达到了O(RC).
另外我这题自己crush的时候为了尽可能的generic, 所以考虑用了anchor分段算法, 但是你看他的crush怎么做的: 直接就是三个一组这样不停的判断就行了; 这个其实也是可以的; 不过这个做法需要的array access比我的多; 当然, 这个就是复杂度上面的小细节了;
不过这个区别感觉也反映出来我的一个毛病, 我现在特别追求写一个写很漂亮很general的大算法, 反而是对这些正常人看起来很intuitive的ad-hoc的操作反而没有什么直觉; 这个问题困扰我其实已经蛮长时间了, 暂时我还没有想到什么好的解决办法;
discussion的一个解法, 算不上特别的优秀其实:
@jun1013 said in AC JAVA Solution easy to understand:
The idea is not to count how many same "candies" are in a row or column, but to check if this candy is eligible for crushing. If any candy is eligible, store the corresponding coordinates in a HashSet.
After traversing the whole board, set the valid candies to "0" then crush (using 2-pointer method in a column).
Here goes the code:
class Solution {
public int[][] candyCrush(int[][] board) {
Set<Coordinates> set = new HashSet<>();
for (int i = 0; i < board.length; i++) {
for (int j = 0; j < board[i].length; j++) {
int cur = board[i][j];
if (cur == 0) continue;
if ((i - 2 >= 0 && board[i - 1][j] == cur && board[i - 2][j] == cur) || // check left 2 candies
(i + 2 <= board.length - 1 && board[i + 1][j] == cur && board[i + 2][j] == cur) || // check right 2 candies
(j - 2 >= 0 && board[i][j - 1] == cur && board[i][j - 2] == cur) || // check 2 candies top
(j + 2 <= board[i].length - 1 && board[i][j + 1] == cur && board[i][j + 2] == cur) || // check 2 candies below
(i - 1 >= 0 && i + 1 <= board.length - 1 && board[i - 1][j] == cur && board[i + 1][j] == cur) || // check if it is a mid candy in row
(j - 1 >= 0 && j + 1 <= board[i].length - 1 && board[i][j - 1] == cur && board[i][j + 1] == cur)) { // check if it is a mid candy in column
set.add(new Coordinates(i, j));
}
}
}
if (set.isEmpty()) return board; //stable board
for (Coordinates c : set) {
int x = c.i;
int y = c.j;
board[x][y] = 0; // change to "0"
}
drop(board);
return candyCrush(board);
}
private void drop(int[][] board) { // using 2-pointer to "drop"
for (int j = 0; j < board[0].length; j++) {
int bot = board.length - 1;
int top = board.length - 1;
while (top >= 0) {
if (board[top][j] == 0) {
top--;
}
else {
board[bot--][j] = board[top--][j];
}
}
while (bot >= 0) {
board[bot--][j] = 0;
}
}
}
}
class Coordinates {
int i;
int j;
Coordinates(int x, int y) {
i = x;
j = y;
}
}
这个是submission最优解: 12(99), 比我的还长
class Solution {
public int[][] candyCrush(int[][] board) {
boolean[][] move = new boolean[board.length][board[0].length];
boolean update = true, tmp = false;
while (update) {
update = false;
//check row and cols, set update true if need update
for (int i = 0; i < board.length; i++) {
tmp = rowCheck(board, i, move);
//System.out.println("\n\trow["+i+"]:"+tmp+"\n");
update = update || tmp;
}
for (int j = 0; j < board[0].length; j++) {
tmp = colCheck(board, j, move);
// System.out.println("\n\tcol["+j+"]:"+tmp+"\n");
update = update || tmp;
}
//printCheck(move);
if (update) {
for (int j = 0; j < board[0].length; j++) {
updateCol(board, j, move);
}
}
//if need update, move board,
}
return board;
}
//colum bottom up check
private boolean colCheck(int[][] board, int col, boolean[][] move) {
boolean res = false;
int len = board.length;
int u = len - 1, d = len - 1;
while (d >= 0) {
if (board[d][col] == 0) break; // [error?] you check col after row, in that case row could make
while (u >= 0 && board[u][col] == board[d][col]) u--;
if (d - u >= 3 && board[d][col] != 0) {
res = true;
for (int i = d; i > u; i--) {
move[i][col] = true;
}
}
d = u;
}
return res;
}
private boolean rowCheck(int[][] board, int row, boolean[][] move) {
boolean res = false;
int len = board[0].length;
int l = 0, r = 0;
while (l < len) {
while (r < len && board[row][r] == board[row][l]) r++;
if (r - l >= 3 && board[row][l] != 0) {
res = true;
for (int i = l; i < r; i++) move[row][i] = true;
}
l = r;
}
return res;
}
private void updateCol(int[][] board, int col, boolean[][] move) {
int up = board.length - 1;
while (up >= 0 && !move[up][col]) up--;
int idx = up;
while (up >= 0) {
if (!move[up][col]) {
move[idx][col] = false;
board[idx--][col] = board[up][col];
}
up--;
}
while (idx >= 0) {
move[idx][col] = false;
board[idx--][col] = 0;
}
}
private void printCheck(boolean[][] check) {
System.out.println("check:");
for (int i = 0; i < check.length; i++) {
for (boolean b: check[i]) System.out.print(b + ", ");
System.out.println();
}
}
}
整个算法的思路感觉实际上是差不多的; 不知道为什么他的这么快; 不过实际上最后的速度差别也不是特别的大, 懒得管了;
Problem Description
This question is about implementing a basic elimination algorithm for Candy Crush.
Given a 2D integer array board representing the grid of candy, different positive integers board[i][j] represent different types of candies. A value of board[i][j] = 0 represents that the cell at position (i, j) is empty. The given board represents the state of the game following the player's move. Now, you need to restore the board to a stable state by crushing candies according to the following rules:
- If three or more candies of the same type are adjacent vertically or horizontally, "crush" them all at the same time - these positions become empty.
- After crushing all candies simultaneously, if an empty space on the board has candies on top of itself, then these candies will drop until they hit a candy or bottom at the same time. (No new candies will drop outside the top boundary.)
- After the above steps, there may exist more candies that can be crushed. If so, you need to repeat the above steps.
- If there does not exist more candies that can be crushed (ie. the board is stable), then return the current board.
You need to perform the above rules until the board becomes stable, then return the current board.
Example 1:
Input: board = [[110,5,112,113,114],[210,211,5,213,214],[310,311,3,313,314],[410,411,412,5,414],[5,1,512,3,3],[610,4,1,613,614],[710,1,2,713,714],[810,1,2,1,1],[1,1,2,2,2],[4,1,4,4,1014]]
Output: [[0,0,0,0,0],[0,0,0,0,0],[0,0,0,0,0],[110,0,0,0,114],[210,0,0,0,214],[310,0,0,113,314],[410,0,0,213,414],[610,211,112,313,614],[710,311,412,613,714],[810,411,512,713,1014]]
Explanation: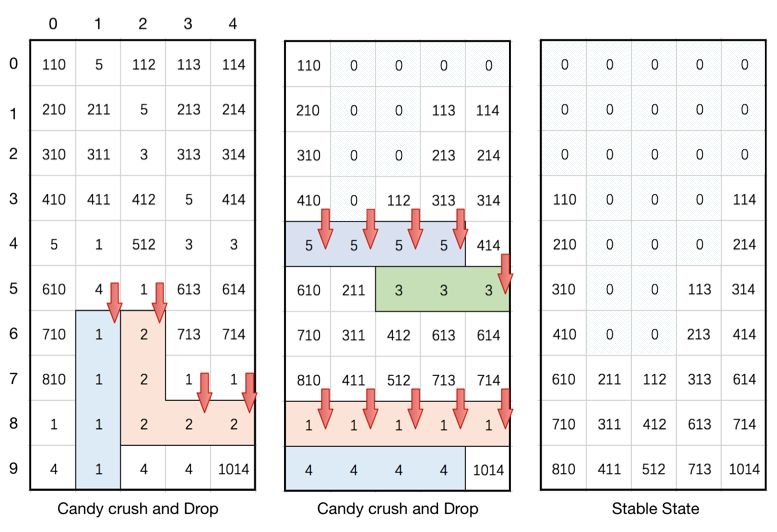
Note:
- The length of board will be in the range [3, 50].
- The length of board[i] will be in the range [3, 50].
- Each board[i][j] will initially start as an integer in the range [1, 2000].
Difficulty:Medium
Total Accepted:1.5K
Total Submissions:2.6K
Contributor:fallcreek
Companies
rubrik
Related Topics
arraytwo pointers
Hint 1
Carefully perform the "crush" and "gravity" steps. In the crush step, flag each candy that should be removed, then go through and crush each flagged candy. In the gravity step, collect the candy in each column and then rewrite the column appropriately. Do these steps repeatedly until there's no work left to do.