BrickWall [source code]
public class BrickWall {
static
/******************************************************************************/
class Solution {
public int leastBricks(List<List<Integer>> wall) {
Map<Integer, Integer> map = new HashMap<>();
for (List<Integer> ls : wall) {
int index = 0;
for (int i = 0; i < ls.size() - 1; i++) {
index += ls.get(i);
Integer count = map.get(index);
if (count == null)
count = 0;
map.put(index, count + 1);
}
}
int n = wall.size(), max = 0;
for (Integer key : map.keySet()) {
max = Math.max(max, map.get(key));
}
return n - max;
}
}
/******************************************************************************/
public static void main(String[] args) {
BrickWall.Solution tester = new BrickWall.Solution();
}
}
大概好像有点想法, 可以写一个粗糙的算法, 但是不确定这个算法就是对的, 决定先写写看, 不纠结, 真正算法要是有问题, 在写的时候再发现, 另外想出路;
结果最后这个方法居然就是对的, 直接就AC了, 整个题目十分钟出头就写完了; 感觉这个题目关键还是看透题目本质的insight; 最后的速度是52ms (10%), 不算快, 但是也看不到优化的地方了? 这个题目不算老, 所以速度这么慢应该是算法本身有毛病, 而不是因为最优解太多了;
另外, 就算是这个不太完美的解法, 还是要依赖于分析例子才能想到; 这个算法的思路其实还是很简单的, 如果你一个线, cut最少的brick, 那么必然是cut最多的edge; 所以直接统计总共每一个edge的位置, 如果一个位置上的edge最多, 那么我们就cut这里; 我感觉这个算法应该是比较完美的了, 不过最后的速度也是慢的很奇怪;
这个是editorial1:
public class Solution {
public int leastBricks(List < List < Integer >> wall) {
int[] pos = new int[wall.size()];
int c = 0, sum = 0, res = Integer.MAX_VALUE;
for (int el: wall.get(0))
sum += el;
while (sum != 0) {
int count = 0;
for (int i = 0; i < wall.size(); i++) {
List < Integer > row = wall.get(i);
if (row.get(pos[i]) != 0)
count++;
else
pos[i]++;
row.set(pos[i], row.get(pos[i]) - 1);
}
sum--;
res = Math.min(res, count);
}
return res;
}
}
这个是一个暴力解法, 最后的复杂度是O(height * width), 这个就很高了(我这个算法是不需要这么高的, 我的算法是O(total number of bricks)).
这个题目, 巧妙解法掌握之后, 回过头来想暴力解法, 反而觉得不是那么好想; 这里他这个算法的设计也一点都不trivial; 总体的思路是, 就是用一个类似人逻辑的思路去做, 就拿着一根线去扫描, 从左到右; 不过既然是要扫描, 因为计算机里面我们能搞的只能是离散值, 所以最后你肯定要决定一个granularity的概念; 他这里的granularity最后采用的是1, 这个也泄露了他这个解法的局限性: 假如我们这里的所有的brick的值都是double这样的, 那么这个方法就没有办法用了, 但是我的办法还可以用;
尽管如此, 他这个解法还是值得学习的, loop1就是扫描线的移动, sum用来记录扫描线当前的位置, 从左到右, 每一个iteration的变化是1; 然后在每一个扫描位置里面, 是iterate on height, 也就是每一个row检查一次, 是否在brick内; 如果是, 那么就count+1, 表明多穿过了一个brick; 最后维护一个最小值;
判断扫描线是否穿过某一个row的brick刚开始看起来可能有点困难, 他这里采用的方法是非常动态的一个方法, 就是直接用一个数组来维护当前扫描线位置, for each row, the index of the brick (within this row) that is being cut. 然后这个pos数组还用来帮助判断是否应该increment count了: 每一个扫描线位置结束之后, 我们将当前被cut的brick的length-1, 类似于一个历史信息流的操作, 这样下一个位置就可以知道whether it is still within that brick;
editorial2就是意识到了上面这个granularity的毛病(1这个值看起来很方便, 但是实际上很arbitrary(当然了, 刚开始想算法的时候, 几个arbitray assumption并不一定是坏事, start somewhere));
public class Solution {
public int leastBricks(List < List < Integer >> wall) {
int[] pos = new int[wall.size()];
int sum = 0, res = Integer.MAX_VALUE;
for (int el: wall.get(0))
sum += el;
while (sum != 0) {
int count = 0, mini = Integer.MAX_VALUE;
for (int i = 0; i < wall.size(); i++) {
List < Integer > row = wall.get(i);
if (row.get(pos[i]) != 0) {
count++;
} else
pos[i]++;
mini = Math.min(mini, row.get(pos[i]));
}
for (int i = 0; i < wall.size(); i++) {
List < Integer > row = wall.get(i);
row.set(pos[i], row.get(pos[i]) - mini);
}
sum -= mini;
res = Math.min(res, count);
}
return res;
}
}
这里做的优化其实就是, instead of 1, 用当前被扫描的所有brick里面的min width来作为granularity; 注意他这里这个最小值, 指的不是原来的input里面给你的这个最小值, 而是在这里他每扫描过一个位置, 就减法之后的最小值, 实际上类似"剩余距离"的最小值; 这个观察其实还是挺聪明的;
注意看现在while里面的body的内容分开成为了两个循环, 一个是更新count, 一个是更新bricks; 因为更新brick的长度的时候要用到一个mini, which is calculated base on the lengths of the bricks cut in the previous round, 所以这里最好的思路还是分开处理;
editorial3的解法基本跟我的一样:
public class Solution {
public int leastBricks(List < List < Integer >> wall) {
HashMap < Integer, Integer > map = new HashMap < > ();
for (List < Integer > row: wall) {
int sum = 0;
for (int i = 0; i < row.size() - 1; i++) {
sum += row.get(i);
if (map.containsKey(sum))
map.put(sum, map.get(sum) + 1);
else
map.put(sum, 1);
}
}
int res = wall.size();
for (int key: map.keySet())
res = Math.min(res, wall.size() - map.get(key));
return res;
}
}
速度比我的稍微快一点: 28(42), 不过也很慢;
discussion最优解, 跟我的算法也是如出一辙:
@DonaldTrump said in I DON'T THINK THERE IS A BETTER PERSON THAN ME TO ANSWER THIS QUESTION:
We want to cut from the edge of the most common location among all the levels, hence using a map to record the locations and their corresponding occurrence. Most importantly, Mexico will pay for it! (I wish)
public class Solution {
public int leastBricks(List<List<Integer>> wall) {
if(wall.size() == 0) return 0;
int count = 0;
Map<Integer, Integer> map = new HashMap<Integer, Integer>();
for(List<Integer> list : wall){
int length = 0;
for(int i = 0; i < list.size() - 1; i++){
length += list.get(i);
map.put(length, map.getOrDefault(length, 0) + 1);
count = Math.max(count, map.get(length));
}
}
return wall.size() - count;
}
}
这个是discussion另外一个不错的解法;
public class Solution {
public int leastBricks(List<List<Integer>> wall) {
int R = wall.size(), min = R;
if (R == 1 && wall.get(0).size() > 1) return 0;
// [0: end, 1: row, 2: col]
PriorityQueue<int[]> pq = new PriorityQueue<>((a, b) -> (a[0] - b[0]));
for (int i = 0; i < R; i++) {
pq.add(new int[] {wall.get(i).get(0), i, 0});
}
while (!pq.isEmpty()) {
int end = pq.peek()[0], count = 0;
while (!pq.isEmpty() && pq.peek()[0] == end) {
count++;
int[] brick = pq.poll();
if (brick[2] < wall.get(brick[1]).size() - 1) {
pq.add(new int[] {end + wall.get(brick[1]).get(brick[2] + 1), brick[1], brick[2] + 1});
}
}
if (!pq.isEmpty()) {
min = Math.min(min, R - count);
}
}
return min;
}
}
这个解法的整体思路其实跟editorial2是一样的; 刚开始我以为这个解法的复杂度不如editorial2的做法, 因为这里PriorityQueue会引入一个lgN的factor进去; 但是你仔细想一下, 这两种解法里面的N是不一样的; 很大可能这两个解法的复杂度是一样的, 都是NlgN, where N is the total number of bricks. 这个复杂度如果你看这个解法还是比较容易分析出来的, 但是如果你看editorial2的算法, 就不是那么容易看出来了; 因为如果你直接看editorial2那个解法, 说难听一点, 你连iteration的个数你都没有办法确定; 也许这两个算法的对比能够引导出一个在复杂度分析上的新的思路? 比如, 我们在之前描述和学习editorial2的时候, 脑子里想的时候是知道说, find min的; 但是真正如果你按照我一直奉行的code line分析的方法, 就非常难看出最后这个NlgN的复杂度; 或许以后看到这种类似find min的类型的算法可以向PriorityQueue分析方法的思路上靠? 也可以算作是一种aggregate analysis?
另外, 对比这两种算法的差别:
- 两个算法其实都完成了一个类似封装的操作; 不同之处在于, 在editorial2里面, 这个封装直接是用一个assoc list来做的, pos就是这个作用, 而这个解法里面, 这个封装直接就是用一个封装来做, 虽然不是一个专门的class, 但是是一个array, 这个也是见过的;
- 另外一点, 可以看到这个算法实际上非常类似BFS? 虽然实际上并不是一回事, 不过感觉或许可以总结出来一些有用的思路;
Problem Description
There is a brick wall in front of you. The wall is rectangular and has several rows of bricks. The bricks have the same height but different width. You want to draw a vertical line from the top to the bottom and cross the least bricks.
The brick wall is represented by a list of rows. Each row is a list of integers representing the width of each brick in this row from left to right.
If your line go through the edge of a brick, then the brick is not considered as crossed. You need to find out how to draw the line to cross the least bricks and return the number of crossed bricks.
You cannot draw a line just along one of the two vertical edges of the wall, in which case the line will obviously cross no bricks.
Example:
Input:
[[1,2,2,1],
[3,1,2],
[1,3,2],
[2,4],
[3,1,2],
[1,3,1,1]]
Output: 2
Explanation:
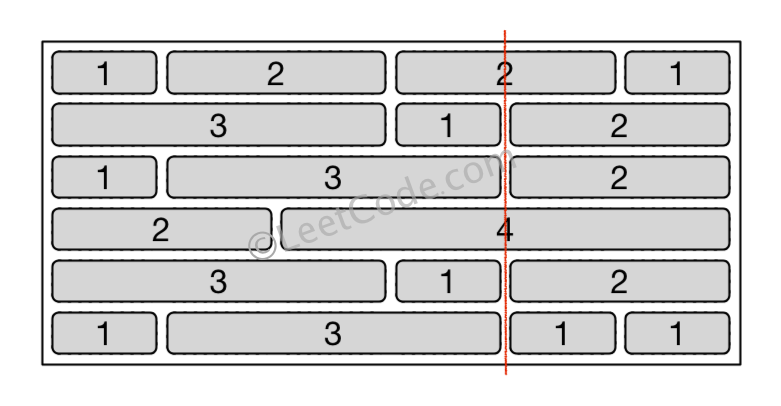
Note:
- The width sum of bricks in different rows are the same and won't exceed INT_MAX.
- The number of bricks in each row is in range [1,10,000]. The height of wall is in range [1,10,000]. Total number of bricks of the wall won't exceed 20,000.
Difficulty:Medium
Total Accepted:10.6K
Total Submissions:23.7K
Contributor: fallcreek
Companies
facebook
Related Topics
hash table