MergeIntervals [source code]
public class MergeIntervals {
static
/******************************************************************************/
class Solution {
public List<Interval> merge(List<Interval> intervals) {
if (intervals == null || intervals.isEmpty ())
return intervals;
Interval[] ar = new Interval[intervals.size ()];
for (int i = 0; i < ar.length; i++)
ar[i] = intervals.get (i);
Arrays.sort (ar, (a, b) -> a.start - b.start);
List<Interval> res = new ArrayList<> ();
int start = ar[0].start, end = ar[0].end;
for (int i = 0; i < ar.length; i++) {
if (ar[i].start <= end) {
end = Math.max (end, ar[i].end);
} else {
res.add (new Interval (start, end));
start = ar[i].start;
end = ar[i].end;
}
}
res.add (new Interval (start, end));
return res;
}
}
/******************************************************************************/
/**
* Definition for an interval.
* public class Interval {
* int start;
* int end;
* Interval() { start = 0; end = 0; }
* Interval(int s, int e) { start = s; end = e; }
* }
*/
public static void main(String[] args) {
MergeIntervals.Solution tester = new MergeIntervals.Solution();
}
}
这个题目最简单的一个思路肯定是直接有一个boolean array, 然后把所有被interval覆盖的地方全都标记, 然后最后一个分段算法跑一遍就行了, 但是这个算法最后这个array可能会很大, 因为直接是给的interval里面的最大值;
array问题, sort也可以, 这题sort一下好像不难, 直接按起点sort, 然后用终点判断与下一个的重合?
算了, 想不到更好的办法了;
最后就用这个思路来做了, 速度是103ms (8%), 明显不给力, submission里面分成了两个梯队, 第一梯队要快很多, 所以估计是有更好的办法的;
editorial
Approach #1 Connected Components [Time Limited Exceeded]
Intuition
If we draw a graph (with intervals as nodes) that contains undirected edges between all pairs of intervals that overlap, then all intervals in each connected component of the graph can be merged into a single interval.
看这意思, 是要DFS? 那会很慢啊, 虽然点子还是不错的;
Algorithm
With the above intuition in mind, we can represent the graph as an adjacency list, inserting directed edges in both directions to simulate undirected edges. Then, to determine which connected component each node is it, we perform graph traversals from arbitrary unvisited nodes until all nodes have been visited. To do this efficiently, we store visited nodes in a Set, allowing for constant time containment checks and insertion. Finally, we consider each connected component, merging all of its intervals by constructing a new Interval with start equal to the minimum start among them and end equal to the maximum end.
This algorithm is correct simply because it is basically the brute force solution. We compare every interval to every other interval, so we know exactly which intervals overlap. The reason for the connected component search is that two intervals may not directly overlap, but might overlap indirectly via a third interval. See the example below to see this more clearly.
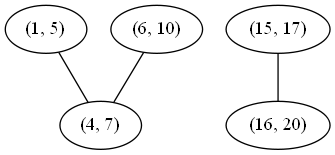
Although (1, 5) and (6, 10) do not directly overlap, either would overlap with the other if first merged with (4, 7). There are two connected components, so if we merge their nodes, we expect to get the following two merged intervals:
(1, 10), (15, 20)
class Solution {
private Map<Interval, List<Interval> > graph;
private Map<Integer, List<Interval> > nodesInComp;
private Set<Interval> visited;
// return whether two intervals overlap (inclusive)
private boolean overlap(Interval a, Interval b) {
return a.start <= b.end && b.start <= a.end;
}
// build a graph where an undirected edge between intervals u and v exists
// iff u and v overlap.
private void buildGraph(List<Interval> intervals) {
graph = new HashMap<>();
for (Interval interval : intervals) {
graph.put(interval, new LinkedList<>());
}
for (Interval interval1 : intervals) {
for (Interval interval2 : intervals) {
if (overlap(interval1, interval2)) {
graph.get(interval1).add(interval2);
graph.get(interval2).add(interval1);
}
}
}
}
// merges all of the nodes in this connected component into one interval.
private Interval mergeNodes(List<Interval> nodes) {
int minStart = nodes.get(0).start;
for (Interval node : nodes) {
minStart = Math.min(minStart, node.start);
}
int maxEnd = nodes.get(0).end;
for (Interval node : nodes) {
maxEnd= Math.max(maxEnd, node.end);
}
return new Interval(minStart, maxEnd);
}
// use depth-first search to mark all nodes in the same connected component
// with the same integer.
private void markComponentDFS(Interval start, int compNumber) {
Stack<Interval> stack = new Stack<>();
stack.add(start);
while (!stack.isEmpty()) {
Interval node = stack.pop();
if (!visited.contains(node)) {
visited.add(node);
if (nodesInComp.get(compNumber) == null) {
nodesInComp.put(compNumber, new LinkedList<>());
}
nodesInComp.get(compNumber).add(node);
for (Interval child : graph.get(node)) {
stack.add(child);
}
}
}
}
// gets the connected components of the interval overlap graph.
private void buildComponents(List<Interval> intervals) {
nodesInComp = new HashMap();
visited = new HashSet();
int compNumber = 0;
for (Interval interval : intervals) {
if (!visited.contains(interval)) {
markComponentDFS(interval, compNumber);
compNumber++;
}
}
}
public List<Interval> merge(List<Interval> intervals) {
buildGraph(intervals);
buildComponents(intervals);
// for each component, merge all intervals into one interval.
List<Interval> merged = new LinkedList<>();
for (int comp = 0; comp < nodesInComp.size(); comp++) {
merged.add(mergeNodes(nodesInComp.get(comp)));
}
return merged;
}
}
卧槽好长..
不过还是有可以学的东西, 比如判断overlap: a.start <= b.end && b.start <= a.end, 没错, 这个方法判断不仅包含普通的overlap, 连一个整个包含另一个的实际上也是涵盖了的; 实际上这个还可以这样写: !(a.start > b.end || b.start > a.end). 但是一般来说你不会想到用这个contradiction来写, 而直接写, 实际上并不是那么trivial;
然后就是用adjacency list来表示graph, 这个也是忘记很久了; adjacency list来表达graph是最常见的方式, 不要忘记了; 然后是undirected edge的表达方法;
然后这个merge的实现, 其实还是有点意思的, 就好像他例子里面说的, 可能是两个interval通过另外一个interval间接相连. 这样的情况用这个graph的情况, 还真的就很好处理; 而且实际的merge的代码也很简单, 直接找最大最小值就行了;
另外, 有一次见到简化版本的iterative DFS; 这个应该掌握了, 实际上很简单; iterative DFS不要求order的时候实际上根本没有难度;
他好像后来给每一个connected component还加了一个数字ID, 但是感觉这一步不是必须的吧? 直接往最后的list里面丢就行了;
复杂度是O(N^2), 因为只有这么多的node, 然后build的时候有一个二重循环(O(E)).
这个方法这一题并不是最好的思路, 又长又慢, 但是要熟悉这么一个用graph来解决interval问题的思路;
Approach #2 Sorting [Accepted]
Intuition
If we sort the intervals by their start value, then each set of intervals that can be merged will appear as a contiguous "run" in the sorted list.
他原文里面还用contradiction证明了一下这个正确性, 不过感觉这个有什么好证明的? 不过, 好像越是straightforward的东西, 越是难证明最后只能依赖于反证法? 大概的思路:
First, suppose that the algorithm at some point fails to merge two intervals that should be merged.
这里说contradiction, 你要能立刻想到, 首先假设的是有两个interval没有被merge, 但是可以被merge, 那么这两个interval是overlap. 看起来到这里就没有条件了; 那么继续思考, 什么叫"没有被merge"? 你这里的证明是针对这个算法的, 所以这个fact最后实际上你要通过分析代码的性质来转化成可以用的性质;
按照这个思路, 假如最后[i]和[j]本来可以merge, 但是最后没有被merge, 那么一定有一个k in (i, j), 使得[i]和[k]没有overlap, 然后[k]和[j]也没有overlap; 然后根据之前代码里面对overlap的定义, 可以解不等式得到矛盾;
这个思路还是比较清晰的, 不过其实不是特别严谨, 严格来说, [i]和[j]之间可能有很多个k, 然后最后合并的应该是一个chain一样的合并所有的不等式; 因为这个算法的代码是一个只能相邻的interval之间比较的过程, 所以只能相邻的两个之间一个一个的比较;
class Solution {
private class IntervalComparator implements Comparator<Interval> {
@Override
public int compare(Interval a, Interval b) {
return a.start < b.start ? -1 : a.start == b.start ? 0 : 1;
}
}
public List<Interval> merge(List<Interval> intervals) {
Collections.sort(intervals, new IntervalComparator());
LinkedList<Interval> merged = new LinkedList<Interval>();
for (Interval interval : intervals) {
// if the list of merged intervals is empty or if the current
// interval does not overlap with the previous, simply append it.
if (merged.isEmpty() || merged.getLast().end < interval.start) {
merged.add(interval);
}
// otherwise, there is overlap, so we merge the current and previous
// intervals.
else {
merged.getLast().end = Math.max(merged.getLast().end, interval.end);
}
}
return merged;
}
}
这个代码比我的简洁, InPlace的做法, 不需要专门搞一个array, 直接通过对之前的interval的修改就行了; start实际上也不需要维护, 我自己的代码里面其实start在维护, 但是实际上除了被add的时候, 根本没有被用到的机会;
@brubru777 said in A simple Java solution:
The idea is to sort the intervals by their starting points. Then, we take the first interval and compare its end with the next intervals starts. As long as they overlap, we update the end to be the max end of the overlapping intervals. Once we find a non overlapping interval, we can add the previous "extended" interval and start over.
Sorting takes O(n log(n)) and merging the intervals takes O(n). So, the resulting algorithm takes O(n log(n)).
I used an a lambda comparator (Java 8) and a for-each loop to try to keep the code clean and simple.
public List<Interval> merge(List<Interval> intervals) {
if (intervals.size() <= 1)
return intervals;
// Sort by ascending starting point using an anonymous Comparator
intervals.sort((i1, i2) -> Integer.compare(i1.start, i2.start));
List<Interval> result = new LinkedList<Interval>();
int start = intervals.get(0).start;
int end = intervals.get(0).end;
for (Interval interval : intervals) {
if (interval.start <= end) // Overlapping intervals, move the end if needed
end = Math.max(end, interval.end);
else { // Disjoint intervals, add the previous one and reset bounds
result.add(new Interval(start, end));
start = interval.start;
end = interval.end;
}
}
// Add the last interval
result.add(new Interval(start, end));
return result;
}
EDIT: Updated with Java 8 lambda comparator.
跟我的代码几乎一模一样;
@stellaxing89 said in A simple Java solution:
Mine is similar, but one difference is I use the iterator to iterate through the original list and then directly modify it, So the final results are already in the "intervals" list.
public List<Interval> merge(List<Interval> intervals) {
if (intervals == null || intervals.isEmpty())
return intervals;
Collections.sort(intervals, new Comparator<Interval>() {
public int compare(Interval i1, Interval i2) {
if (i1.start != i2.start) {
return i1.start - i2.start;
}
return i1.end - i2.end;
}
});
ListIterator<Interval> it = intervals.listIterator();
Interval cur = it.next();
while (it.hasNext()) {
Interval next = it.next();
if (cur.end < next.start) {
cur = next;
continue;
} else {
cur.end = Math.max(cur.end, next.end);
it.remove();
}
}
return intervals;
}
用的iterator, 我并不是很熟悉;
看起来很neat, 但是实际上有问题:
@brubru777 said in A simple Java solution:
I see just a little problem with this code. It works fine with a LinkedList but with an ArrayList, remove() takes linear time. In the worst case, that'd make the algorithmm quadratic. So, that makes the algorithm dependent on the type of list used.
反正我也不会, 正好;
另外, editorial2的原型:
@leogogogo said in A simple Java solution:
My concise Java code using Stack:
public List<Interval> merge(List<Interval> intervals) {
Stack<Interval> stack = new Stack();
Collections.sort(intervals, (a,b) -> a.start - b.start);
for(Interval it: intervals){
if(stack.isEmpty() || it.start > stack.peek().end) stack.push(it);
else{
stack.peek().end = Math.max(it.end, stack.peek().end);
}
}
return new ArrayList(stack);
}
@nrl said in A simple Java solution:
Was asked to solve this question by FB without using the new operator (ie creating new objects). Below is my solution in O(1) space.
public class Solution {
public List<Interval> merge(List<Interval> itv) {
if (itv == null) throw new IllegalArgumentException();
Collections.sort(itv, new Comparator<Interval>(){
@Override
public int compare(Interval a, Interval b) {
if (a.start == b.start) return b.end - a.end;
return a.start - b.start;
}
});
int i = 0;
while (i < itv.size() - 1) {
Interval a = itv.get(i), b = itv.get(i + 1);
if (a.end >= b.start) {
a.end = Math.max(a.end, b.end);
itv.remove(i + 1);
}
else i++;
}
return itv;
}
}
所以其实上面那个直接在input list里面直接修改的做法还真的不是花拳绣腿, 真的会有公司问这个要求的;
@brubru777 said in A simple Java solution:
remove is an O(n) operation. So, in the worst case, you would end up with a quadratic algorithm instead of linearithmic.
And if the list is a LinkedList, get(i) and get(i + 1) can also take linear time (not 100% sure about this one but it seems very plausible), making this implementation quite inefficient (quadratic again).
The for-each loop, on the other hand, takes linear time to access all elements whatever list is used (ArrayList or LinkedList).
@lchen77 said in C++ 10 line solution. easing understanding:
vector<Interval> merge(vector<Interval>& ins) {
if (ins.empty()) return vector<Interval>{};
vector<Interval> res;
sort(ins.begin(), ins.end(), [](Interval a, Interval b){return a.start < b.start;});
res.push_back(ins[0]);
for (int i = 1; i < ins.size(); i++) {
if (res.back().end < ins[i].start) res.push_back(ins[i]);
else
res.back().end = max(res.back().end, ins[i].end);
}
return res;
}
@sydy71 said in C++ 10 line solution. easing understanding:
this is a really good solution. Another naive approach is to use the "insert interval function", which will result in o(n^2) time complexity.
还没做到这一题, 不知道说的什么意思;
@StefanPochmann said in 7 lines, easy, Python:
Just go through the intervals sorted by start coordinate and either combine the current interval with the previous one if they overlap, or add it to the output by itself if they don't.
def merge(self, intervals):
out = []
for i in sorted(intervals, key=lambda i: i.start):
if out and i.start <= out[-1].end:
out[-1].end = max(out[-1].end, i.end)
else:
out += i,
return out
@D_shaw said in Beat 98% Java. Sort start & end respectively.:
The idea is that for the result distinct Interval, the latter one's start must > previous one's end.
public List<Interval> merge(List<Interval> intervals) {
// sort start&end
int n = intervals.size();
int[] starts = new int[n];
int[] ends = new int[n];
for (int i = 0; i < n; i++) {
starts[i] = intervals.get(i).start;
ends[i] = intervals.get(i).end;
}
Arrays.sort(starts);
Arrays.sort(ends);
// loop through
List<Interval> res = new ArrayList<Interval>();
for (int i = 0, j = 0; i < n; i++) { // j is start of interval.
if (i == n - 1 || starts[i + 1] > ends[i]) {
res.add(new Interval(starts[j], ends[i]));
j = i + 1;
}
}
return res;
}
等于说特么又是这个解法; 同样底下没有证明;
大概画了一个图, 感觉应该模糊的能解释这个意思;
大概意思就是, 无论是哪种类型的overlap, 当你sort之后, 你要关注的只是紫色的pairing就行了, 不用管这个pairing之前是不是对应于同一个interval;
我在下面贴的:
@vegito2002 said in Beat 98% Java. Sort start & end respectively.:
I encountered this same approach in one other interval-related problem and posted some formalized proof for this solution there, but unfortunately I can't seem to find that for now. Here is some intuitive explanation:

blue is interval, red is start, green is end, purple is the pairing after sorting, that is a purple corresponds to one
starts[i], ends[i]pair after sorting.As you can see, there are two kinds of overlapping: intersection and comprehension. No matter what kind it is, you can just pretend, after the sorting, that each purple pair actually is an interval, even though it does not really corresponds to any original blue interval. Then you do the
start, endcompare as you normally use to judge interval overlapping. The end result is the same anyway.
上面这个方法就是submission的最优解, 第一梯队的解法, 搞半天好多人都用的这个方法? 不过真正面试的时候我感觉用这个思路很危险, 能正儿八经的, 甚至只是大概的证明这个思路的人其实都很少;
这个是第一梯队后面一点的解法:
class Solution {
public List<Interval> merge(List<Interval> intervals) {
List<Interval> res = new ArrayList<>();
if (intervals == null || intervals.size() == 0) return res;
Collections.sort(intervals, new Comparator<Interval>(){
public int compare(Interval i1, Interval i2) {
return Integer.compare(i1.start, i2.start);
}
});
int s = intervals.get(0).start;
int e = intervals.get(0).end;
for (Interval i : intervals) {
if (i.start > e) {
res.add(new Interval(s, e));
s = i.start;
e = i.end;
} else {
e = Math.max(e, i.end);
}
}
res.add(new Interval(s, e));
return res;
}
}
好像也没什么区别? 可能就是我单独搞了一个array的原因? 因为在构建这个array的过程当中, 你反复的调用get, 这个可能最后导致了一个N^2的速度; 看来这个东西真的不是虚张声势, 真的会被坑的;
我当时之所以想要先转化为array主要是因为不知道有Collections.sort这个东西; 不过话说回来, 这个sort到底是怎么实现的? 难道系统sort一个collection的时候不依赖array? 不对啊, 就算是依赖array, 你的问题是你get调用的太多了, 不是sort占用时间;
Problem Description
Given a collection of intervals, merge all overlapping intervals.
For example,
Given [1,3],[2,6],[8,10],[15,18],
return [1,6],[8,10],[15,18].
Difficulty:Medium
Total Accepted:179.4K
Total Submissions:566.9K
Contributor:LeetCode
Companies
googlefacebookmicrosoftbloomberglinkedintwitteryelp
Related Topics
arraysort
Similar Questions
Insert IntervalMeeting RoomsMeeting Rooms IITeemo AttackingAdd Bold Tag in StringRange ModuleEmployee Free TimePartition Labels