RangeSumQueryMutable [source code]
public class RangeSumQueryMutable {
static
/******************************************************************************/
class NumArray {
int[] tree;
int n;
public NumArray(int[] nums) {
this.n = nums.length;
this.tree = new int[2 * n];
for (int i = 0; i < n; i++)
tree[i + n] = nums[i];
for (int i = n - 1; i > 0; i--) // reversed order is critical
tree[i] = tree[2 * i] + tree[2 * i + 1];
}
public void update(int i, int val) {
i += n;
tree[i] = val;
while (i > 0) { // include 1, exclude 0
int parent = i / 2; // find [2k, 2k+1] alignment
tree[parent] = tree[2 * parent] + tree[2 * parent + 1];
i = parent;
}
}
public int sumRange(int i, int j) {
i += n;
j += n;
int sum = 0;
while (i <= j) { // can include i==j
if ((i & 1) == 1) // if i == 2k+1
sum += tree[i++];
if ((j & 1) == 0) // if j == 2k'
sum += tree[j--];
i /= 2;
j /= 2;
}
return sum;
}
}
/******************************************************************************/
/**
* Your NumArray object will be instantiated and called as such:
* NumArray obj = new NumArray(nums);
* obj.update(i,val);
* int param_2 = obj.sumRange(i,j);
*/
public static void main(String[] args) {
}
}
Google最喜欢考的线段树, 了解一下;
大概思考了一下, 也没什么思路, 不想了;
上面实现用的是editorial3的线段树写法; 确实有点tricky; 不过理解了之后代码非常好记;
然而这个居然速度之后又146(17)! 我的天, 不讲理了是不是, 一点collection都没有, 居然还这么慢;
更恶心一点这连个while循环还可以改成for循环, 不过没意思了, while循环本身也更加清晰;
editorial
Approach #1 (Naive) [Time Limit Exceeded]
Algorithm
A trivial solution for Range Sum Query - RSQ(i, j) is to iterate the array from index i to j and sum each element.
private int[] nums;
public int sumRange(int i, int j) {
int sum = 0;
for (int l = i; l <= j; l++) {
sum += data[l];
}
return sum;
}
public int update(int i, int val) {
nums[i] = val;
}
// Time Limit Exceeded
Approach #2 (Sqrt decomposition) [Accepted]
...
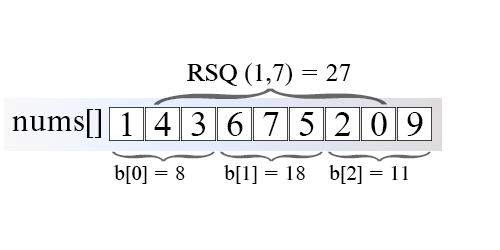
感觉就是一个分bucket之后来降低更新影响范围从而提速的技巧, 其他地方好像见到过;
private int[] b;
private int len;
private int[] nums;
public NumArray(int[] nums) {
this.nums = nums;
double l = Math.sqrt(nums.length);
len = (int) Math.ceil(nums.length/l);
b = new int [len];
for (int i = 0; i < nums.length; i++)
b[i / len] += nums[i];
}
public int sumRange(int i, int j) {
int sum = 0;
int startBlock = i / len;
int endBlock = j / len;
if (startBlock == endBlock) {
for (int k = i; k <= j; k++)
sum += nums[k];
} else {
for (int k = i; k <= (startBlock + 1) * len - 1; k++)
sum += nums[k];
for (int k = startBlock + 1; k <= endBlock - 1; k++)
sum += b[k];
for (int k = endBlock * len; k <= j; k++)
sum += nums[k];
}
return sum;
}
public void update(int i, int val) {
int b_l = i / len;
b[b_l] = b[b_l] - nums[i] + val;
nums[i] = val;
}
// Accepted
代码思路还是比较清晰的; 复杂度是O(sqrt(N))的, 这个还是比较好理解的; 如果i和j在一个block里面, 就是sqrt(N), 最坏情况是sqrtN-2个b的值都选择, 然后两头两个block单独都要计算, 也就是sum(0, N-1)这个query;
最后代码写的时候小心一点就行了; 另外注意为什么选择bucket的大小是sqrtN这个应该也是比较清晰的了;
Approach #3 (Segment tree) [Accepted]
Algorithm
Segment tree is a very flexible data structure, because it is used to solve numerous range query problems like finding minimum, maximum, sum, greatest common divisor, least common denominator in array in logarithmic time.
...

所以我之前的理解是比较naive的, 保存的不是针对一个segment, 而是用aggregate这个词, 更加准确;
注意这里的区分, 35这个node把0..5给分开了, 但是35本身是不占用位置的, 也就是分开之后的0..1 + 2..5合起来还是0..5的;
Segment tree could be implemented using either an array or a tree. For an array implementation, if the element at index i is not a leaf, its left and right child are stored at index 2i and 2i+1 respectively.
这个有点像heap的做法;
...
Segment Tree can be broken down to the three following steps:
- Pre-processing step which builds the segment tree from a given array.
- Update the segment tree when an element is modified.
- Calculate the Range Sum Query using the segment tree.
int[] tree;
int n;
public NumArray(int[] nums) {
if (nums.length > 0) {
n = nums.length;
tree = new int[n * 2];
buildTree(nums);
}
}
private void buildTree(int[] nums) {
for (int i = n, j = 0; i < 2 * n; i++, j++)
tree[i] = nums[j];
for (int i = n - 1; i > 0; --i)
tree[i] = tree[i * 2] + tree[i * 2 + 1];
}
void update(int pos, int val) {
pos += n;
tree[pos] = val;
while (pos > 0) {
int left = pos;
int right = pos;
if (pos % 2 == 0) {
right = pos + 1;
} else {
left = pos - 1;
}
// parent is updated after child is updated
tree[pos / 2] = tree[left] + tree[right];
pos /= 2;
}
}
public int sumRange(int l, int r) {
// get leaf with value 'l'
l += n;
// get leaf with value 'r'
r += n;
int sum = 0;
while (l <= r) {
if ((l % 2) == 1) {
sum += tree[l];
l++;
}
if ((r % 2) == 0) {
sum += tree[r];
r--;
}
l /= 2;
r /= 2;
}
return sum;
}
这个build的做法是跟sedgwick上面heapsort那里的做法很相似的; 注意顺序一定要是从右边往左边;
算了来不及了不看Sedgwick的代码了, 直接看这里给的这个代码;
文章作者并没有完全理解这个build过程的巧妙之处; 只是单纯给了一个文字描述, 尤其是他对于这个倒序操作的精妙支出只字未提;
注意一点, 这个结构跟heap确实非常类似, 但是不是! 有区别; heap本质上为了维护sorted顺序, 各种swap, swim, sink反而更麻烦; 这里只要一个倒序保证Bottom-Up就行了; 记住他这里这个模板;
然后update里面, 注意他left和right的操作, 反正就是要把left, right调整到2k, 2k+1这个区间就行了;
然后整个一直往上走, 过程倒不是很复杂;
复杂度是lgN这个分析方法是类似heap当时的, 因为array是compact的所以tree是balanced的, height就有上限了;
大概看了代码, 也画了这两个草稿, 还是很难理解, 尤其是sum; 没想到最后居然是读操作更难以理解;


想了一下, 感觉还是太飘了, 根本没有认真去思考, 也就是之前讲过的, 理解一个算法, 要从trace的角度去理解; 我这里基本就是根据代码去看, 其实根本没有从自己建造trace的角度去理解他;
那么我们就从build开始去理解; 这里给的这个例子也挺好的, 就用这个;

build就是这个过程, 还是比较直观的;
然后update的时候, 应该先找到leaf位置, 因为你update的都是一个leaf node: 对于你这个client来说, 你只能看到nums原来的, 比如0..n-1这个长度的内容, 这个tree内部的internal node对你来说是不可见的; 所以当你说我希望nums[pos]=val的时候, 针对的就是一个leaf; 但是我们现在在内部的tree数组里面, leaf需要向后offset一下; 这个不难理解;
然后pos就记录自己当前的位置; 记住, 在tree数组里面, array index就对应了你在tree里面的位置; 不过我感觉这个表达的一个弱点是没有办法合理的看到level的显示;
那么我们知道pos代表我们在tree里面的位置, 我们就先找到当前位置该干什么; 因为是一个binary的结构, 先找到自己的sibling, 然后分别自称为left和right, 然后找到parent, 更新parent的值, 很简单, 然后走向parent, 继续操作; update这个过程这样用直观的人逻辑来描述一下, 其实挺简单的;
sum才是比较难的地方;
我们还是看这个tree, 还是看sum[1..4]这个query; 这个sum比较难以理解的一个地方是, 为什么要判断奇偶性;
首先, l和r肯定还是在leaf位置; 然后注意一个问题, 最后实际上这个线段树最后操作, 都是一个两两一个单位的; 所以当你要求l..r的时候, 你要首先要找到multiples of 2的subrange; 如果l是奇数, 那么l+1肯定就是align到了2k的位置; 同理, 如果r是偶数, 那么r-1肯定就是align到了2k+1的位置;
这个能造成什么区别呢; l自己在2k+1的位置的时候, 其实l不用管后面l+1..r范围内怎么样, 这些肯定是上面的internal node能够解决; l因为自己不属于中间部分了, 所以要把自己先加到sum里面去; r也是, 如果r自己是2k, 那么l..r-1的部分就可以放心的(因为是2的倍数)向上递交, 但是r自己是没有办法递交上去的; 所以先把r自己给+到sum里面去;
如果l是偶数, r是奇数, 就什么也不用管, 自动向上走就行了;
题外话, 讲实话这题一开始感觉还真的没有想到用线段树来做, 感觉没有开花那题那么明显; 但是也跟最开始说的一样, 只要是range aggregate的, 都可以考虑这个方法;
理解上面的这个align的操作, 基本就是把l..r按照长度分成类似(1)+2+2+...+2+(1)这样的结果, 中间的这么多2, 是可以往上传递的, 但是两头的落单的1, 要先处理掉;
我们这里sum[1..4]这个其实是一个最坏情况: 第一层有两次+操作; 一般来说, 你可以把这个例子搞大一点, 会发现, 后面这个循环, 每一个iteration, l和r至多只有一个人会触发+操作; 所以最后height才能够bound住时间;
无论这一层有l和r当中谁触发了+操作, 反正正常的+, +完之后向内align (保证align之后的l是一个2k, r是一个2k'+1). 这样现在的l..r就肯定在同一个subtree里面;
哎, 这个东西还是有点tricky; 不过最起码现在感觉trace记下来了, 代码按说应该是能写出来了;
注意header里面能够取等号: 反正相等的时候l和r当中只有一个会发生+操作; 所以无所谓;
另外, 这里其实他不是为了模仿heap, 我感觉就是想炫技吧. 毕竟array表示tree这个其实用的很少; 而且还有限制条件: 要compact(才能保证tree balanced), 正好这个条件这里满足, 所以就用了;
注意, 你再看上面的tree图形, 我们是没有一个明显的在node里面保存区间值的, 完全就是依靠binary对应的这个奇偶性操作来移动啊干什么的; 这个就真的是有点, 太炫技了;
后面翻了一下discuss, 正常的版本的线段树其实是有人写的;
说实话这个算法还是不是特别懂, 尤其是你sum[0..4]的时候, 你自己走一下trace, 看到在node3和4的时候, 就停止了; 那么这个算法是怎么知道这个情况下就应该停止的? 因为0..4其实是multiples of 2, 但是最后实际上不在一个subtree里面;
然而即使是这样, 这个算法居然自动就知道什么时候应该停止; 还是觉得很不可思议;
另外说一个题外话, 下面的线段树做法其实都还挺简单的, 但是这题有一个地方, 这题介绍的这些线段树做法, 其实都不适合开花那一题, 那一题是要不停的有新的split操作的; 而不是一开始建立好一个tree, 然后后面查询就行了;
public class NumArray {
class SegmentTreeNode {
int start, end;
SegmentTreeNode left, right;
int sum;
public SegmentTreeNode(int start, int end) {
this.start = start;
this.end = end;
this.left = null;
this.right = null;
this.sum = 0;
}
}
SegmentTreeNode root = null;
public NumArray(int[] nums) {
root = buildTree(nums, 0, nums.length-1);
}
private SegmentTreeNode buildTree(int[] nums, int start, int end) {
if (start > end) {
return null;
} else {
SegmentTreeNode ret = new SegmentTreeNode(start, end);
if (start == end) {
ret.sum = nums[start];
} else {
int mid = start + (end - start) / 2;
ret.left = buildTree(nums, start, mid);
ret.right = buildTree(nums, mid + 1, end);
ret.sum = ret.left.sum + ret.right.sum;
}
return ret;
}
}
void update(int i, int val) {
update(root, i, val);
}
void update(SegmentTreeNode root, int pos, int val) {
if (root.start == root.end) {
root.sum = val;
} else {
int mid = root.start + (root.end - root.start) / 2;
if (pos <= mid) {
update(root.left, pos, val);
} else {
update(root.right, pos, val);
}
root.sum = root.left.sum + root.right.sum;
}
}
public int sumRange(int i, int j) {
return sumRange(root, i, j);
}
public int sumRange(SegmentTreeNode root, int start, int end) {
if (root.end == end && root.start == start) {
return root.sum;
} else {
int mid = root.start + (root.end - root.start) / 2;
if (end <= mid) {
return sumRange(root.left, start, end);
} else if (start >= mid+1) {
return sumRange(root.right, start, end);
} else {
return sumRange(root.right, mid+1, end) + sumRange(root.left, start, mid);
}
}
}
}
node定义跟我一开始想的差不多, 区间是要保存的, 看到没, 这个跟上面数组做法有区别; 然后就是多保存一个sum, 也就是problem-dependent的aggregate信息就行了;
这个是一个recursive的版本, 所以就很棒, 很好理解, 不过update用的是mutation recursion而不是Sedgwick提倡的parent relinking & returned recursion的组合拳; 反正也还可以把; 虽然他实际过程还是一个recursive的update;
看他的build, 可以看到这个是一个Top-Down的过程; 这个实际上才是一个比较正宗的线段树. 讲道理, editorial那个解法还是有点奇怪;
然后分区间还是用的闭区间, 这个让人安心;
build的时候倒是用了returned relinking组合拳;
理解这个Top-Down recursion的关键, 就是理解base case: 最本质的操作是什么; 这里是在长度等于1的时候停下来, 直接返回一个新node;
update在root本身是global的情况下, 还是加了一个node参数, 就是因为想要recursive的使用;
然后update这个思路其实跟我当时自己脑子里潦草勾勒的思路是差不多的, 就是你这个index要跟一个segment的mid进行比较, 然后找kid;
然后整个就很简单了;
最后再更新一下sum, 这个就跟Sedgwick上面最后统一更新size一样的思路;
想想Sedgwick书上真的是什么都讲了;
sum的base case就是一个hit: 要求的这个区间, 正好是当前node的区间; 这个就算是不乐观的情况(比如给的区间正好真的有一个对应的node被你找到了), 最后还是会hit, 因为最后长度为1的时候, 了伐 node也会hit这一条;
然后其他情况下就是最简单的recursion;
妈耶, 这个写法简单多了好嘛. 如果我写的话, 我会考虑update改成returned recursion, 不过无伤大雅; 而且这个写法还有一个好处就是复杂度分析更加简单;
反正, 都学习一下吧; array来做tree的, 真的见得不多;
Nice solution! For those who are not familiar with segment tree (like myself), this post might be helpful: Segment Tree | Set 1 (Sum of given range)
我没看了, 这会儿没时间; 而且我还是更加喜欢结合例子来理解怎么使用; 碰到题目要用的时候, 再说;
另外一个教程:
@ElementNotFoundException Actually, I find this one is better: https://www.topcoder.com/community/data-science/data-science-tutorials/range-minimum-query-and-lowest-common-ancestor/#Segment_Trees
另外下面其实有人说, 这个所谓的线段树, 如果按照这个实现方式, 这就是一个BST啊, 根本没有任何神秘的地方; key的形式稍微特殊一点, 是一个区间, 然后就这点门道了;
还是很有意义的一个题目;
build的时候记得上来就要先new一个node出来: 你无论如何, 在build的过程中, 这个internal node你一定要按照PreOrder的顺序先建立出来;
下面有一个聪明的优化:
Maybe we don’t need to return range sum until (root.start==start && root.end==end), when root.start>=start && root.end<=end, then the sum of this node can be used directly, just return root.sum.
I think it much quicker.
Here’s my implementation using segment tree.
public class NumArray {
class segmentNode{
int start;
int end;
int sum;
segmentNode left;
segmentNode right;
public segmentNode(int start,int end){
this.start = start;
this.end = end;
this.left = null;
this.right = null;
this.sum = 0;
}
}
segmentNode node;
int[] nums;
public NumArray(int[] nums) {
this.nums = new int[nums.length];
for(int i=0;i<nums.length;i++)
this.nums[i]=nums[i];
this.node = buildtree(nums,0,nums.length-1);
}
void update(int i, int val) {
int diff = nums[i]-val;
nums[i]=val;
if(node!=null)
nupdate(node,i,diff);
}
public int sumRange(int i, int j) {
return node==null?0:sum(node,i,j);
}
public segmentNode buildtree(int[] nums,int start,int end){
if(start>end) return null;
segmentNode root = new segmentNode(start,end);
if(start == end)
root.sum = nums[start];
else{
int mid = start + (end-start)/2;
root.left = buildtree(nums,start,mid);
root.right = buildtree(nums,mid+1,end);
root.sum = root.left.sum+root.right.sum;
}
return root;
}
public int sum(segmentNode root, int start, int end){
if(root==null||start>root.end || end<root.start) return 0;
if(start<=root.start && end>=root.end) return root.sum;
int left = sum(root.left,start,end);
int right = sum(root.right,start,end);
return left+right;
}
public void nupdate(segmentNode root, int index,int diff){
if(root==null||index>root.end||index<root.start) return;
if(index>=root.start && index<=root.end) root.sum-=diff;
nupdate(root.left,index,diff);
nupdate(root.right,index,diff);
}
}
这个优化我刚开始根本没看懂, 还认为是错的: 因为你看他sum的range根本就不变;
不过他这里其实是观察到了当你sum的时候, 整个tree的区间结构已经组织好了, 你根本没有必要把search range进行对应的拆分; 最后其实类似一个什么呢, 类似一个比如0..6里面找1..5, 最后分成了:
0..6:
0..3:
0..1:
0 -> 0
1 -> sum[1]
-> sum[1];
2..3: shorcut -> sum[2..3]
-> sum[1..3]
4..6:
4..5: shortcut -> sum[4..5]
6 -> 0
-> sum[4..5]
-> sum[1..5]
这个过程应该还是很直观的, 可以看到他这个shortcut触发了两次, 最后1..5实际上分成了1 + 2..3 + 4..5这样三个小段, 实际上有点类似一个integer拆分成为sum of powers of 2的思路; 还是有点slick的;

A normal binary tree is actually enough to implement this, there’s no need to include start and end in the tree node. Here’s an implementation in C#.
这个人的说法是正确的, 因为editorial那个数组做法里面, 根本没有存过任何跟区间有关系的东西; 直接就是一个binary本身的各种操作就行了;
public class NumArray {
private TreeNode SegTree;
private int[] Arr;
public NumArray(int[] nums) {
if (nums==null || nums.Length==0) { return; }
SegTree = new TreeNode(0);
Arr = nums;
ConstructST(SegTree, nums, 0, Arr.Length-1);
}
public void Update(int i, int val) {
if (Arr==null) { return; }
int diff = val - Arr[i];
Arr[i] = val;
UpdateTree(SegTree, i, diff, 0, Arr.Length-1);
}
private void UpdateTree(TreeNode root, int i, int diff, int st, int ed){
if (i<st || i>ed){
return;
}
root.val += diff;
if (st==ed) { return; }
int mid = st + (ed-st)/2;
UpdateTree(root.left, i, diff, st, mid);
UpdateTree(root.right, i, diff, mid+1, ed);
}
public int SumRange(int i, int j) {
if (Arr==null) { return 0; }
return Search(SegTree, i, j, 0, Arr.Length-1);
}
private int Search(TreeNode root, int i, int j, int st, int ed ){
if (i<=st && j>=ed) {
return root.val; // this is the range sum
}
if (i>ed || j<st) {
return 0;
}
int mid = st + (ed-st)/2;
return Search(root.left, i, j, st, mid) + Search(root.right, i, j, mid+1, ed);
}
private int ConstructST(TreeNode root, int[] nums, int st, int ed){
if (st==ed){
root.val = nums[st];
return root.val;
}
root.left = new TreeNode(0); // either 0 or 2 children
root.right = new TreeNode(0); // we can see that this will be a full binary tree
int mid = st + (ed-st)/2;
int sum = ConstructST(root.left, nums, st, mid)
+ ConstructST(root.right, nums, mid+1, ed);
root.val = sum;
return root.val;
}
private class TreeNode{
public int val;
public TreeNode left;
public TreeNode right;
public TreeNode(int val){
this.val = val;
}
}
}
construct写的比较有意思: 站在一个root, 先把自己的两个child给制造出来, 然后再recurse下去, 让他们自己去设置value; 下行的时候, 把node一个一个new出来, 上行的时候, 把value一个一个的更新上去; 这个设定其实有点不错的;
不知道为什么他要求必须是full tree; 往后继续看的话;
这个人也用diff来update, 为什么他们都喜欢这个; 注意观察一下这个diff的方向; ar[i] + diff = val, 所以diff应该+给old, 得到new value;
下面的root.val += diff也验证了这一点; 其他的就是recursion, update没有太多花样;
他最后sum这里的门道, 你看他这个search函数, 本身函数方面用path一样的方式去维护i..j和start..end两个区间; 在一个node的时候, start..end其实自动就对应上了我们这个node本来拥有的区间范围, 因为当时制作的时候, 就是这么一个很简单的二分拆分, 所以你search的时候, 也按照同样的规则二分维护这个start..end区间就行了;
这个观察还是挺有意思的; 然后他也用了上面那个人那种提前退出的方法(如果search range包含root range, 就直接返回root的sum); 一个power of 2拆分的思路;
哎, 感觉这几个方法看下来, 其实比editorial那个炫技的学到的东西更多;
Here is an alternative implementation with reference to GeekForGeeks (http://www.geeksforgeeks.org/segment-tree-set-1-sum-of-given-range/), which uses array as tree. I think it’s not bad even though a little complicated somewhere.
For example, idx*2+1/+2 are children of current “node”. Meanwhile since each position of array only saves the sum, params ‘from’, ‘to’ and ‘idx’ are required to track where we are. Here is the code. Just for your reference.
代码没贴了, 非常的复杂; 反正数组tree的方法, 掌握editorial那个就可以了; 本身代码也简单; geeks4geeks这个代码实在是太乱七八糟了;
不过有一点好, 是用的recursion, 所以好理解一些; 不好的一点是他不是用i's children at 2i and 2i+1这个计算, 他计算稍微还shift了一点, 这个就不太好; 毕竟1based这个计算也是Sedgwick书上推荐的计算方法;
算了, 贴了代码, 以后有空再看吧:
private int[] st;
private int end;
public NumArray(int[] nums) {
if (nums.length == 0) return;
int height = (int) (Math.ceil(Math.log(nums.length) / Math.log(2)));
st = new int[2 * (int) Math.pow(2, height) - 1];
end = nums.length - 1;
build(nums, 0, nums.length - 1, 0);
}
void update(int i, int val) {
modify(0, end, 0, i, val);
}
public int sumRange(int i, int j) {
return query(0, end, 0, i, j);
}
private int build(int[] nums, int from, int to, int idx) {
if (from == to) {
st[idx] = nums[from];
return st[idx];
}
int mid = from + (to - from) / 2;
st[idx] = build(nums, from, mid, idx * 2 + 1) + build(nums, mid + 1, to, idx * 2 + 2);
return st[idx];
}
private void modify(int from, int to, int idx, int i, int val) {
if (from == to) {
st[idx] = val;
return;
}
int mid = from + (to - from) / 2;
if (i <= mid) modify(from, mid, idx * 2 + 1, i, val);
else modify(mid + 1, to, idx * 2 + 2, i, val);
st[idx] = st[idx * 2 + 1] + st[idx * 2 + 2];
}
private int query(int from, int to, int idx, int lower, int upper) {
if (lower <= from && to <= upper) return st[idx];
int mid = from + (to - from) / 2;
if (upper <= mid) return query(from, mid, idx * 2 + 1, lower, upper);
if (mid < lower) return query(mid + 1, to, idx * 2 + 2, lower, upper);
return query(from, mid, idx * 2 + 1, lower, upper) + query(mid + 1, to, idx * 2 + 2, lower, upper);
}
最后多总结一句, 这题那个包含就退出的优化, 其实是核心关键点; 有了这个优化之后, sum才能够lgN; 可以自己画图, 比如在0..6当中找1..5这个例子, 你会发现在大部分的node, 有了这个优化之后的结果, 其实就等于每一个node只会走两个child当中的一个, 也就是branching变成了只有1, 这样最后的复杂度才会跟height挂钩; 暂时没时间就不画图了; 反正这个trace最好是在一个树状图上面看, 比较直观; 发生return的node标记出来, 能够很清楚的看出来一个level只选择一个node;
UNFINISHED
Problem Description
Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive.
The update(i, val) function modifies nums by updating the element at index i to val.
Example:
Given nums = [1, 3, 5]
sumRange(0, 2) -> 9
update(1, 2)
sumRange(0, 2) -> 8
Note:
- The array is only modifiable by the update function.
- You may assume the number of calls to update and sumRange function is distributed evenly.
Difficulty:Medium
Total Accepted:44.2K
Total Submissions:195.3K
Contributor:LeetCode
Related Topics
binary indexed treesegment tree
Similar Questions
Range Sum Query - ImmutableRange Sum Query 2D - Mutable