FindTheDuplicateNumber [source code]
public class FindTheDuplicateNumber {
static
/******************************************************************************/
class Solution {
public int findDuplicate(int[] nums) {
int t = 0, h = 0;
// do-while is better here
do {
t = nums[t];
h = nums[nums[h]];
} while (t != h);
h = 0;
while (t != h) {
t = nums[t];
h = nums[h];
}
return t;
}
}
/******************************************************************************/
public static void main(String[] args) {
FindTheDuplicateNumber.Solution tester = new FindTheDuplicateNumber.Solution();
}
}
这个题目比看起来要稍微难一点, 因为不虚modify, 所以不能用InPlace flag的技巧, 而且又不允许用extra space, 所以整个就没有办法做类似count之类的东西? 用recursion行不行? 规避space的限制; 这个也是一个你应该知道的规避space限制的技巧;
感觉这个题目可能要换一个思路; 这个题目首先空间限制很严格, 所以限制了一定的做法上的方向; 另外, 这个题目时间允许你到N^2, 我感觉是在暗示这个题目最后正确答案的思路其实有点反常规, 不一定是之前那些题目的做法;
注意读题的时候要仔细, 这题跟以前经常做的fully-assoc的题目其实有区别: 这题并没有说[1,n]内的所有的数字都会出现; 不过即使是这样, 这种设定其实也是可以导致用bucket array来做了; 虽然这一题本身是不允许了;
想了半天毫无思路, 直接看答案了;
最后是模仿这editorial的龟兔赛跑算法写出来了上面的解法, 最后的速度是1ms (58%).
editorial
Note
The first two approaches mentioned do not satisfy the constraints given in the prompt, but they are solutions that you might be likely to come up with during a technical interview. As an interviewer, I personally would not expect someone to come up with the cycle detection solution unless they have heard it before.
这个是一个很好的提示: 面试的时候真的是要从笨办法开始的;
Approach #1 Sorting [Accepted]
class Solution {
public int findDuplicate(int[] nums) {
Arrays.sort(nums);
for (int i = 1; i < nums.length; i++) {
if (nums[i] == nums[i-1]) {
return nums[i];
}
}
return -1;
}
}
这个是不满足题目要求, 但是他就是放这里给你看一下;
Approach #2 Set [Accepted]
class Solution {
public int findDuplicate(int[] nums) {
Set<Integer> seen = new HashSet<Integer>();
for (int num : nums) {
if (seen.contains(num)) {
return num;
}
seen.add(num);
}
return -1;
}
}
Approach #3 Floyd's Tortoise and Hare (Cycle Detection) [Accepted]
龟兔赛跑可以解这题? 没有什么想法;
class Solution {
public int findDuplicate(int[] nums) {
// Find the intersection point of the two runners.
int tortoise = nums[0];
int hare = nums[0];
do {
tortoise = nums[tortoise];
hare = nums[nums[hare]];
} while (tortoise != hare);
// Find the "entrance" to the cycle.
int ptr1 = nums[0];
int ptr2 = tortoise;
while (ptr1 != ptr2) {
ptr1 = nums[ptr1];
ptr2 = nums[ptr2];
}
return ptr1;
}
}
自己看一下文章的解释, 这个算法是把这个问题reduce到了cycle detection问题;
这个题目的这个龟兔赛跑他是refer到了另外一个题目上面去了, 但是那个题目其实我还没有做过, 所以我干脆这里就直接分析一下这个问题;
首先, 为什么想到用龟兔赛跑? 龟兔赛跑算法一般来说是比较常见用于graph题目里面的; 这里他就是看到了一个index, value的pair可以看成是一个graph的edge的表示; 那么什么可以trigger你到这个思路? 事实上, 这里的这个equal domain的特点, 我们以前也总结过了, 但是这里就是一个新的思路; 以前看到equal domain问题自然的想的比较多的是类似value as index的技术; 这里看来, 另外一个思考方向就是转换成graph.
one out multi in
首先, 注意这题的这个graph形式, 优于是从一个array得到的, 所以有一个隐藏性质, 就是每一个node只有一个out; 事实上, 这个设定也符合大部分的graph题目的设定;
那么既然知道是graph, 跟这题本身要你求的的东西之间又有什么关系呢? 为什么知道duplicate是cycle? 事实上, duplicate value (注意, 不是index), 代表至少有一个node, 有more than one inward edges.
但是这个实际上好像还是没有办法很好的证明这个graph里面一定有cycle? editorial自己讲的还是挺好的, 因为每一个entry的value对应的都是一个实际存在的index, 那么最后你是可以无限traverse的, 所以一定有cycle; 换成graph的讲法, 每一个node都有一个out; 你总共有n个node(0可以不管, 不影响), 每一个都要有自己的out, 那么每一个都要有自己的child, 最后肯定是有cycle的;
知道有cycle之后, 就标准的龟兔赛跑就行了; 他这里的做法, 起点是nums[0], 但是实际上直接用0自己也可以;
找到intersection点之后, 下一步就是找到cycle entrance, 这个要参考另外一个图里面用到的一个图例:
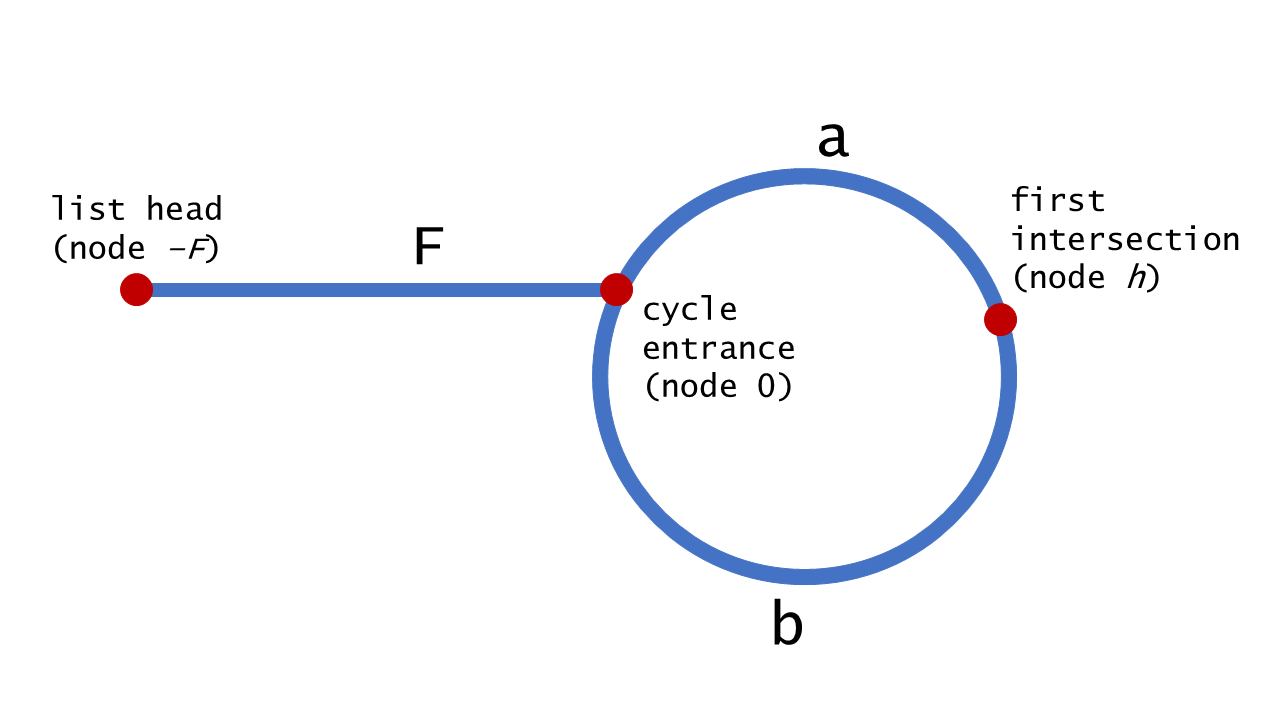
这个图上面是可以证明F和b是相等的; 知道这个之后, 第二个循环的内容就容易理解了; 两个相同速度的指针, 一起跑, 最后汇合的地方肯定就是entrance;
一个小的注意点就是两个循环的起点要一致, 要么都是0, 要么就都是[0].
discussion最优解:
@echoxiaolee said in My easy understood solution with O(n) time and O(1) space without modifying the array. With clear explanation.:
The main idea is the same with problem Linked List Cycle II,https://leetcode.com/problems/linked-list-cycle-ii/. Use two pointers the fast and the slow. The fast one goes forward two steps each time, while the slow one goes only step each time. They must meet the same item when slow==fast. In fact, they meet in a circle, the duplicate number must be the entry point of the circle when visiting the array from nums[0]. Next we just need to find the entry point. We use a point(we can use the fast one before) to visit form begining with one step each time, do the same job to slow. When fast==slow, they meet at the entry point of the circle. The easy understood code is as follows.
int findDuplicate3(vector<int>& nums)
{
if (nums.size() > 1)
{
int slow = nums[0];
int fast = nums[nums[0]];
while (slow != fast)
{
slow = nums[slow];
fast = nums[nums[fast]];
}
fast = 0;
while (fast != slow)
{
fast = nums[fast];
slow = nums[slow];
}
return slow;
}
return -1;
}
这题其实还是可以用binary search来做的, 复杂度也可以接受:
@mehran said in Two Solutions (with explanation): O(nlog(n)) and O(n) time , O(1) space, without changing the input array:
This solution is based on binary search.
At first the search space is numbers between 1 to n. Each time I select a number
mid(which is the one in the middle) and count all the numbers equal to or less thanmid. Then if thecountis more thanmid, the search space will be[1 mid]otherwise[mid+1 n]. I do this until search space is only one number.Let's say
n=10and I selectmid=5. Then I count all the numbers in the array which are less than equalmid. If the there are more than5numbers that are less than5, then by Pigeonhole Principle (https://en.wikipedia.org/wiki/Pigeonhole_principle) one of them has occurred more than once. So I shrink the search space from[1 10]to[1 5]. Otherwise the duplicate number is in the second half so for the next step the search space would be[6 10].class Solution(object): def findDuplicate(self, nums): """ :type nums: List[int] :rtype: int """ low = 1 high = len(nums)-1 while low < high: mid = low+(high-low)/2 count = 0 for i in nums: if i <= mid: count+=1 if count <= mid: low = mid+1 else: high = mid return lowThere's also a better algorithm with
O(n)time. Please read this very interesting solution here:
http://keithschwarz.com/interesting/code/?dir=find-duplicate
他的证明当中有一个问题, 被Stefan指出来了:
@StefanPochmann said in Two Solutions (with explanation): O(nlog(n)) and O(n) time , O(1) space, without changing the input array:
If the there are more than 5 numbers that are less than 5, then by Pigeonhole Principle one of them has occurred more than once. [...]. Otherwise the duplicate number is in the second half
While that's all correct, it's incomplete. The pigeonhole principle is only one way. It does tell you that there's a duplicate if there are "too many" items. But it doesn't tell you that there isn't a duplicate if there aren't "too many" items. So how do you know the duplicate is in the second half?
I'd put it this way:
Let
countbe the number of elements in the range1 .. mid, as in your solution.If
count > mid, then there are more thanmidelements in the range1 .. midand thus that range contains a duplicate.If
count <= mid, then there aren+1-countelements in the rangemid+1 .. n. That is, at leastn+1-midelements in a range of sizen-mid. Thus this range must contain a duplicate.
Or less formally:
We know that the whole range is "too crowded" and thus that the first half or the second half of the range is too crowded (if both weren't, then neither would be the whole range). So you check to know whether the first half is too crowded, and if it isn't, you know that the second half is.
Also, better say "less than or equal to 5", not just "less than 5".
Btw, you could also use
count = sum(i <= mid for i in nums)
or even directlyif sum(i <= mid for i in nums) <= mid:.
这个观察力还是很敏锐的;
这题实际上最后想到用binary search做的人其实还是挺多的, 这个是随便贴的另外一个:
public int findDuplicate(int[] nums) {
int low = 1, high = nums.length - 1;
while (low <= high) {
int mid = (int) (low + (high - low) * 0.5);
int cnt = 0;
for (int a : nums) {
if (a <= mid) ++cnt;
}
if (cnt <= mid) low = mid + 1;
else high = mid - 1;
}
return low;
}
submission看到一个另类的写法:
class Solution {
public int findDuplicate(int[] nums) {
int n = nums.length;
int slow = n;
int fast = n;
do{
slow = nums[slow-1];
fast = nums[nums[fast-1]-1];
}while(slow != fast);
slow = n;
while(slow != fast){
slow = nums[slow-1];
fast = nums[fast-1];
}
return slow;
}
}
注意他这里的起点, 比如1,1,4,3,2这样的, 他的起点是5; 这个最后导致第一个iteration在实质上只导致fast比slow快了一步. 不知道这个是什么妖路子. 算法本身是对的, 但是这样倒着做, 感觉很多前面分析的理念就不适用了;
Problem Description
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Note:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than O(n^2).
- There is only one duplicate number in the array, but it could be repeated more than once.
Credits:
- Special thanks to @jianchao.li.fighter for adding this problem and creating all test cases.
Difficulty:Medium
Total Accepted:93.8K
Total Submissions:213K
Contributor:LeetCode
Companies
bloomberg
Related Topics
arraytwo pointersbinary search
Similar Questions
First Missing PositiveSingle NumberLinked List Cycle IIMissing NumberSet Mismatch