Combinations [source code]

public class Combinations {
static
/******************************************************************************/
class Solution {
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> res = new ArrayList<> ();
        Deque<Integer> path = new ArrayDeque<> ();
        boolean[] used = new boolean[n + 1];
        search (n, k, res, path, used);
        return res;
    }

    void search (int n, int k, List<List<Integer>> lss, Deque<Integer> path, boolean[] used) {
        if (k == 0) {
            lss.add (new ArrayList<> (path));
            return;
        }
        for (int i = n; i >= 1; i--) {
            if (used[i])
                continue;
            used[i] = true;
            path.push (i);
            search (i - 1, k - 1, lss, path, used);
            path.pop ();
            used[i] = false;
        }
    }
}
/******************************************************************************/

    public static void main(String[] args) {
        Combinations.Solution tester = new Combinations.Solution();
    }
}

首先想到的一个问题是, 我们在计算的时候, 包括记录used这些信息的时候, 可以直接就全都用0based来处理, 最后真正需要add到result里面的时候, 再临时转换成1based的, 这样避免混淆;

不过这题其实无所谓, 因为这题并没有一个explicit的array, 所以并不存在一个index和value之间的混淆;

既然固定了size, 那么直接用size based的backtracking好像合理一些, 虽然element based的其实也可以? 直接判断res.size跟K的关系就行了;

说是一个找combination的问题, 但是最后让你返回list而不是set, 其实就是考察你去重的能力; 注意, 这个能力还是很重要的, 因为如果不去重, 可能算法速度会被大大的拖累;

另外, 这题因为是combination, 不是permutation, 所以如果每一个node都从1开始重新搜, 只依靠used来去重, 最后是不行的, 比如1 2和2 1就会重新出现: used只能排除一个数字被多次使用, 对于这种duplicate没有作用; 所以这里要用一个类似start的东西来enforce order: 每一个position之间选择的数字之间要有order; 我最后没有单独用一个start, 直接用n来, 然后在node里面反过来走, 这样节省一个参数位置;

不免要和permutation问题对比: 为什么当时不需要用start(即使是允许需要去重的PermutationII)? 是因为1 2和2 1在permutation问题下面, 是不同的解; 而且PermutationII问题当时的去重其实是在同一个数字之内才enforce order(用的也不是start方法, 而是neighbor order的方法), 所以跟这里其实并不是一回事;

最后速度是32ms (48%);

2018-02-15 18:41:45 突然发现一个问题, 上面的代码, used根本就是多余的:

class Solution {  
    public List<List<Integer>> combine(int n, int k) {  
        List<List<Integer>> res = new ArrayList<> ();  
        Deque<Integer> path = new ArrayDeque<> ();  
        search (n, k, res, path);  
        return res;  
    }  

    void search (int n, int k, List<List<Integer>> lss, Deque<Integer> path) {  
        if (k == 0) {  
            lss.add (new ArrayList<> (path));  
            return;  
        }  
        for (int i = n; i >= 1; i--) {  
            path.push (i);  
            search (i - 1, k - 1, lss, path);  
            path.pop ();  
        }  
    }  
}

照样AC;

所以实际上start扮演的就是一个类似used的角色, 这个也是之前就解释过了的;

根据后面的题目来看, size based的写法的时候(iteration内部本身还有一个循环fanning), 一般start的作用就是跟used重合的; 但是如果是element based的写法, 一般参数里面虽然也经常会有一个index, 但是这个index并不是一个start的概念(只是一个当前iteration对应的element的index), 所以这种写法往往还无法彻底丢弃used;

没有editorial;

https://leetcode.com/problems/combinations/discuss/27002/Backtracking-Solution-Java

    public static List<List<Integer>> combine(int n, int k) {  
        List<List<Integer>> combs = new ArrayList<List<Integer>>();  
        combine(combs, new ArrayList<Integer>(), 1, n, k);  
        return combs;  
    }  
    public static void combine(List<List<Integer>> combs, List<Integer> comb, int start, int n, int k) {  
        if(k==0) {  
            combs.add(new ArrayList<Integer>(comb));  
            return;  
        }  
        for(int i=start;i<=n;i++) {  
            comb.add(i);  
            combine(combs, comb, i+1, n, k-1);  
            comb.remove(comb.size()-1);  
        }  
    }

标准写法;

Please check out my more precise version, based on the following fact:

• the valid range for the 1st position is [1, n-k+1]
• the valid range for the i-th position is [number we selected for previous position+1, n-k+1+i]

public class Solution {  
    public List<List<Integer>> combine(int n, int k) {  
        List<List<Integer>> ans = new ArrayList<>();  
        dfs(ans, new ArrayList<Integer>(), k, 1, n-k+1);  
        return ans;  
    }  

    private void dfs(List<List<Integer>> ans, List<Integer> list, int kLeft, int from, int to) {  
        if (kLeft == 0) { ans.add(new ArrayList<Integer>(list)); return; }  
        for (int i=from; i<=to; ++i) {  
            list.add(i);  
            dfs(ans, list, kLeft-1, i+1, to+1);  
            list.remove(list.size()-1);  
        }  
    }  
}

看起来很犀利, 但是实际上是无用操作: 真正碰到那种, 比如在(n, k) = (4, 2)的时候, 假如[0]选择了3, 那么最后下一个position的node自动就会因为循环范围无效而被prune掉;

https://leetcode.com/problems/combinations/discuss/27019/A-short-recursive-Java-solution-based-on-C(nk)C(n-1k-1)+C(n-1k)

Basically, this solution follows the idea of the mathematical formula C(n,k)=C(n-1,k-1)+C(n-1,k).

Here C(n,k) is divided into two situations. Situation one, number n is selected, so we only need to select k-1 from n-1 next. Situation two, number n is not selected, and the rest job is selecting k from n-1.

public class Solution {  
    public List<List<Integer>> combine(int n, int k) {  
        if (k == n || k == 0) {  
            List<Integer> row = new LinkedList<>();  
            for (int i = 1; i <= k; ++i) {  
                row.add(i);  
            }  
            return new LinkedList<>(Arrays.asList(row));  
        }  
        List<List<Integer>> result = this.combine(n - 1, k - 1);  
        result.forEach(e -> e.add(n));  
        result.addAll(this.combine(n - 1, k));  
        return result;  
    }  
}

这个就是一个用returned recursion rather than mutation recursion来做的思路, 也不陌生; 严格来说这个可以认为是一个element based的手法;

This recursion will calculate duplicates, see C(3,2) on this image

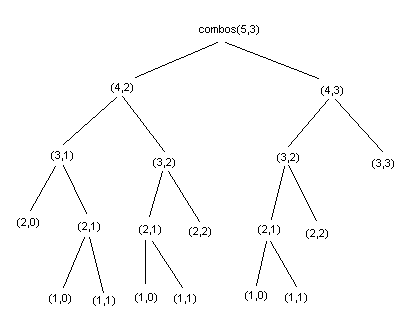
看起来很正确, 实际上有毛病: 这个人只看node, 所以认为是重复, 但是实际上, 我们找的是path, 所以你必须要看edge;

可以看到这两个(3,2)并不是重复, 因为他们的prefix(parent)不一样;

但是有一个问题, 好像是有些重复计算, 既然是returned recursion, 严格来说这个算法是可以加memo的;

那么普通的backtracking会不会出现这样的重复计算呢(这个应该交repeating, 叫duplicate有点不严谨)? 肯定是有的, 两个算法的tree几乎是差不多的;

尝试给这个算法加memo, 但是发现, 如果memo的value是类似这里的collection of collections, 那么实际的操作很难处理:

public class Solution {  
    Map<String, List<List<Integer>>> map = new HashMap<> ();  
    String header = "";  
    boolean MD = true;  

    public List<List<Integer>> combine(int n, int k) {  
        String old_header = header;  
        header += "  ";  
        if (MD) System.out.printf ("%sn:(%d), k(%d)\tENTER\t%s\n", header, n, k, Printer.wrap (map.toString (), 96));  
        String key = String.format ("%d|%d", n, k);  
        List<List<Integer>> res;  
        if (map.containsKey (key)) {  
            if (MD) System.out.println (header + 1);  
            res = new ArrayList<> (map.get (key));  
        } else if (k == n || k == 0) {  
            if (MD) System.out.println (header + 2);  
            res = new ArrayList<> ();  
            List<Integer> row = new ArrayList<>();  
            for (int i = 1; i <= k; ++i) {  
                row.add(i);  
            }  
            res.add (row);  
        } else {  
            if (MD) System.out.println (header + 3);  
            res = combine (n - 1, k - 1);  
            res.forEach (e -> e.add (n));  
            res.addAll (combine (n - 1, k));  
        }  
        map.put (key, new ArrayList<> (res));  
        if (MD) System.out.printf ("%sn:(%d), k:(%d)\tEXIT %s\t%s\n", header, n, k, Printer.wrap (res.toString(), 95), Printer.wrap (map.toString (), 96));  
        header = old_header;  
        return res;  
    }  
}

上面的方法是带debug的; trace太大就不贴了; 问题就是, 虽然我这里保证没有人修改Map里面的list of list copy, 但是这个并不够: lss虽然是不会被修改, 但是lss的不同copy之间实际上共享里面所有的ls的指针, 所以最后的修改还是会波及到其他的node; 暂时想不到解决这个问题的好办法: 如果自己手动deep copy lss, 那么带来的overhead就太得不偿失了;

注意他这里的forEach的用法; 参数应该是一个function; 网上找到的其他的例子items.forEach(System.out::println);, 应该是这个意思了; 这个双冒号是什么意思?

等价的操作是: items.forEach(item->System.out.println(item));.

原来是java8新加的: http://www.baeldung.com/java-8-double-colon-operator

Very simply put, when we are using a method reference – the target reference is placed before the delimiter :: and the name of the method is provided after it.

Function<Computer, Integer> getAge = Computer::getAge;  
Integer computerAge = getAge.apply(c1);

List inventory = Arrays.asList(  
  new Computer( 2015, "white", 35), new Computer(2009, "black", 65));  
inventory.forEach(ComputerUtils::repair);

双冒号前面也可以是一个object而不是一个class:

Computer c1 = new Computer(2015, "white");  
Computer c2 = new Computer(2009, "black");  
Computer c3 = new Computer(2014, "black");  
Arrays.asList(c1, c2, c3).forEach(System.out::print);  

Computer c1 = new Computer(2015, "white", 100);  
Computer c2 = new MacbookPro(2009, "black", 100);  
List inventory = Arrays.asList(c1, c2);  
inventory.forEach(Computer::turnOnPc);  

@Override  
public Double calculateValue(Double initialValue){  
    Function<Double, Double> function = super::calculateValue;  
    Double pcValue = function.apply(initialValue);  
    return pcValue + (initialValue/10) ;  
}

@FunctionalInterface  
public interface InterfaceComputer {  
    Computer create();  
}  

InterfaceComputer c = Computer::new;  
Computer computer = c.create();

BiFunction<Integer, String, Computer> c4Function = Computer::new;   
Computer c4 = c4Function.apply(2013, "white");

@FunctionalInterface  
interface TriFunction<A, B, C, R> {   
    R apply(A a, B b, C c);   
    default <V> TriFunction<A, B, C, V> andThen( Function<? super R, ? extends V> after) {   
        Objects.requireNonNull(after);   
        return (A a, B b, C c) -> after.apply(apply(a, b, c));   
    }   
}  

TriFunction <Integer, String, Integer, Computer> c6Function = Computer::new;  
Computer c3 = c6Function.apply(2008, "black", 90);

Function <Integer, Computer[]> computerCreator = Computer[]::new;  
Computer[] computerArray = computerCreator.apply(5);

One point to note about method reference is that they provide a way to refer to a method, they don’t execute the method.

https://leetcode.com/problems/combinations/discuss/26992/Short-Iterative-C++-Answer-8ms

class Solution {  
public:  
    vector<vector<int>> combine(int n, int k) {  
        vector<vector<int>> result;  
        int i = 0;  
        vector<int> p(k, 0);  
        while (i >= 0) {  
            p[i]++;  
            if (p[i] > n) --i;  
            else if (i == k - 1) result.push_back(p);  
            else {  
                ++i;  
                p[i] = p[i - 1];  
            }  
        }  
        return result;  
    }  
};

用数字进位的思路来做, 很有意思;

刚开始以为看懂了, 然后重新思考了一下代码, 发现没看懂; 就自己开始画trace; 画完了大概好像是看懂了; 这个其实就是一个类似backtracking的循环操作; 你肯定要问了, 不对啊, backtracking什么时候可以用循环写了? 之前总结过一次, recursion相对于iteration, 一个不可替代的优势是, recursion, 尤其是backtracking是不需要提前知道循环的层数的; 但是这题就不同, 这题我们是知道循环的层数的: 用size based的思路, 层数就是tree的level的数量, 就是K; 所以直接可以用循环来写; 这个按理说其实好像不是数字进位的做法;

另外, 我们以前说过, recursion的另外一个优势是可以undo, 但是这里看来, iteration实现undo好像也挺简单的哈, 至少是某些特定情况下;

另外, 你有没有理解这个算法是怎么完成去重的? 这个是在他的第三个branch里面实现的, 当当前[i]的++没有造成特殊的结果(溢出什么或者到达leaf什么的), 那么我们就认定当前的[i]没有问题, 那么直接走到下一层, 然后让下一层先直接copy当前这个[i]位置, 也就是parent的数字, 然后下一个iteration会自动给他++, 这个其实跟我们recursion里面把当前的i+1当成下一个level的start, 是一样的思想;

总体来说这个算法写的还是很干净利落的;

https://leetcode.com/problems/combinations/discuss/27032/Iterative-Java-solution

Hi guys!

The idea is to iteratively generate combinations for all lengths from 1 to k. We start with a list of all numbers <= n as combinations for k == 1. When we have all combinations of length k-1, we can get the new ones for a length k with trying to add to each one all elements that are <= n and greater than the last element of a current combination.

I think the code here will be much more understandable than further attempts to explain. :) See below.

这句话很装逼啊;

Hope it helps!

public class Solution {  
    public List<List<Integer>> combine(int n, int k) {  
        if (k == 0 || n == 0 || k > n) return Collections.emptyList();  
        List<List<Integer>> combs = new ArrayList<>();  
        for (int i = 1; i <= n; i++) combs.add(Arrays.asList(i));  
        for (int i = 2; i <= k; i++) {  
            List<List<Integer>> newCombs = new ArrayList<>();  
            for (int j = i; j <= n; j++) {  
                for (List<Integer> comb : combs) {  
                    if (comb.get(comb.size()-1) < j) {  
                        List<Integer> newComb = new ArrayList<>(comb);  
                        newComb.add(j);  
                        newCombs.add(newComb);  
                    }  
                }  
            }  
            combs = newCombs;  
        }  
        return combs;  
    }  
}

这种做法的算法好像以前是见过一次的, 并不是特别的新鲜; 而且好像底下评论说这个算法现在已经是TLE了; 相比于普通的recursion之类的做法, 这个算法的一个问题是, 比如list.get这样的操作, 实际上是很expensive的;

当然, 一个关键的问题还是去重, 他这个去重的做法实际上就是保证list的order; 虽然说set本身是不要求order的, 但是跟这个是两回事;

另外, 如果我们需要的是一个类似last的位置的信息, 那么是不是可以用Deque或者Stack之类的东西来accummulate?

下面一个人给出的优化:

public List<List<Integer>> combine(int n, int k) {  
    if (n == 0 || k == 0 || k > n) return Collections.emptyList();  
    List<List<Integer>> res = new ArrayList<List<Integer>>();  
    for (int i = 1; i <= n + 1 - k; i++) res.add(Arrays.asList(i));  
    for (int i = 2; i <= k; i++) {  
        List<List<Integer>> tmp = new ArrayList<List<Integer>>();  
        for (List<Integer> list : res) {  
            for (int m = list.get(list.size() - 1) + 1; m <= n - (k - i); m++) {  
                List<Integer> newList = new ArrayList<Integer>(list);  
                newList.add(m);  
                tmp.add(newList);  
            }  
        }  
        res = tmp;  
    }  
    return res;  
}

大概的差别就是, OP原来的算法是对于每一个j, 都要走一遍所有之前的list, 然后看情况append上去; 但是这个优化的做法是, 先for each list, 然后直接思考这个list可以append的是那些数字; 这个方法好像确实需要像他这里这样, 比较严格的计算一下每一个list可以append的数字的上下限;

submission最优解:4(95):

class Solution {  
    public List<List<Integer>> combine(int n, int k) {  
        List<List<Integer>> resultList = new ArrayList<>();  
        List<Integer> list = new ArrayList<>();  

        combineHelper(1, n, k, list, resultList);  
        return resultList;  
    }  

    public void combineHelper(int start, int n, int k, List<Integer> list, List<List<Integer>> resultList) {  
        if ( k == 0 ) {  
            // case #1  
            resultList.add(new ArrayList<>(list));  
            return;  
        }  
        if ( n - start + 1 < k ) {  
            // case #2  
            return;  
        }  

        // add start to list  
        list.add(start);  
        combineHelper(start + 1, n, k - 1, list, resultList);  
        // remove start from list  
        list.remove(list.size() - 1);  
        combineHelper(start + 1, n, k, list, resultList);  
    }  
}

这个其实就是很简单的element based的写法的backtracking, 为什么速度差这么多? 我的size based的写法足足要32ms, 这个只要4; 我觉得, 可能跟OJ给的test case有关系; size based的做法最后的深度是K, 而element based的做法最后的深度是N. 不对, N肯定大于K啊, 所以size based的按理来说不是应该肯定更快的吗?

想不通, 真的想不通; size based的应该是(base是fanning): N^K, element based的应该是2^N, 难道是这个原因? size based的方法base太大导致的? 有可能; 对这个问题要适当长一个心眼;

另外这个时候才回想起来, 这题实际上给的nums里面(implicit的)实际上是不包含duplicate的, 虽然一直以来也是无所谓;

我突然想到是不是有这样一个操作: 我们可以判断K跟N/2的关系, 如果K比N/2大, 那么我们直接搜(N, N - K), 然后最后对得到的结果来一个线性处理? 不知道这个小优化是否值得;

Problem Description

Given two integers n and k, return all possible combinations of k numbers out of 1 ... n.

For example,
If n = 4 and k = 2, a solution is:

[  
  [2,4],  
  [3,4],  
  [2,3],  
  [1,2],  
  [1,3],  
  [1,4],  
]

Difficulty:Medium
Total Accepted:136.5K
Total Submissions:334K
Contributor:LeetCode
Related Topics
backtracking
Similar Questions
Combination SumPermutations