AndroidUnlockPatterns [source code]
public class AndroidUnlockPatterns {
static
/******************************************************************************/
class Solution {
static int N = 3;
static int[][] increments1 = {
{-1,0}, {1,0}, {0, -1}, {0,1},
{-1, -1}, {-1, 1}, {1, -1}, {1, 1},
};
static int[][] increments2 = {
{-1, -2}, {-1,2},{1,-2},{1,2},
{-2,-1}, {-2,1}, {2, -1}, {2, 1},
};
public int numberOfPatterns(int m, int n) {
int res = 0;
res += dfs (1, 1, new boolean[3][3], 0, m, n, 0) +
4 * (dfs (0, 0, new boolean[3][3], 0, m, n, 0) +
dfs (0, 1, new boolean[3][3], 0, m, n, 0));
return res;
}
int dfs (int x, int y, boolean[][] visited, int count, int m, int n, int pathLen) {
if (!isValidXY(x, y) || visited[x][y])
return count; // can't return 0 here!
visited[x][y] = true;
pathLen++;
if (m <= pathLen && pathLen <= n)
count++; //critical position: pre-leaf is better than leaf here
for (int[] incre : increments1) {
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
if (isValidXY (x + incre[0], y + incre[1]) && visited[x + incre[0]][y + incre[1]])
count = dfs (x + 2 * incre[0], y + 2 * incre[1], visited, count, m, n, pathLen);
}
for (int[] incre : increments2)
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
visited[x][y] = false; // subtle but critical
return count;
}
boolean isValidXY (int x, int y) {
return !(x < 0 || x >= 3 || y < 0 || y >= 3);
}
}
/******************************************************************************/
public static void main(String[] args) {
AndroidUnlockPatterns.Solution tester = new AndroidUnlockPatterns.Solution();
int[] inputs = {
1, 1, 9,
2, 2, 56,
3, 3, 320,
1, 3, 385,
4, 4, 1624,
5, 5, 7152,
6, 6, 26016,
7, 7, 72912,
8, 8, 140704,
9, 9, 140704,
2, 6, 35168,
};
for (int i = 0; i < inputs.length / 3; i++) {
int m = inputs[3 * i], n = inputs[3 * i + 1], ans = inputs[3 * i + 2];
System.out.println (Printer.separator ());
int output = tester.numberOfPatterns (m, n);
System.out.printf ("%d and %d -> %s, expected: %d\n",
m, n, Printer.wrapColor (output + "", output == ans ? "green" : "red"), ans
);
}
}
}
这一题实际上降低了一点难度, 就是不允许重复, 而实际的解锁pattern, 是允许重复的; 这题如果允许重复, 那么难度会上升不少;
写代码的时候不要忙着Premature Optmization, 比如想要节省一个临时变量这样的操作; 你做题目的时候就应该是模拟你面试的时候的情形, 真正面试的时候, 只要你代码能过就行了, 没有人会管你是不是多用了几个临时变量;
class Solution {
static int[][] increments1 = {
{-1,0}, {1,0}, {0, -1}, {0,1},
{-1, -1}, {-1, 1}, {1, -1}, {1, 1},
};
static int[][] increments2 = {
{-1, -2}, {-1,2},{1,-2},{1,2},
{-2,-1}, {-2,1}, {2, -1}, {2, 1},
};
public int numberOfPatterns(int m, int n) {
Set<Integer> paths = new HashSet<> ();
boolean[][] visited;
for (int k = m; k <= n; k++) {
for (int i = 0; i < 3; i++) {
for (int j = 0; j < 3; j++) {
visited = new boolean[3][3];
dfs (i, j, paths, visited, 0);
}
}
}
return paths.size ();
}
void dfs (int x, int y, Set<Integer> paths, boolean[][] visited, int step, int {
if (!isValidXY(x, y) || visited[x][y])
return;
visited[x][y] = true;
10 + (3 * x + y + 1);
step--;
for (int[] incre : increments1) {
dfs (x + incre[0], y + incre[1], paths, visited, step,
if (isValidXY (x + incre[0], y + incre[1]) && visited[x + incre[0]][y + incre[1]])
dfs (x + 2 * incre[0], y + 2 * incre[1], paths, visited, step,
}
for (int[] incre : increments2)
dfs (x + incre[0], y + incre[1], paths, visited, step,
visited[x][y] = false; // subtle but critical
if (step == 0)
paths.add ( //critical position: pre-leaf is better than leaf here
}
boolean isValidXY (int x, int y) {
return !(x < 0 || x >= 3 || y < 0 || y >= 3);
}
}
最后写出来的就是这个算法, 不过很可惜, 超时了; 当然了, 我也知道这个题目是有比较低端的枚举的办法来cheat OJ的, 不过为了面试的目的, 是没有意义的;
虽然说这个算法超时了, 不过还是学到了很多东西; 尤其是comment标注出来的两个位置, 都是非常容易犯错的地方;
一个问题在于我一开始一直以为不需要undo visited, 这个是因为我忽略了一个问题, 虽然这里是一个DFS算法, 但是我们的目标不是一个类似寻找connected component的问题, 而是一个寻找path. 这个才是这个问题的本质; 所以你的visited你应该想想到底用来mark什么, 如果仅仅是用来mark一个DFS走过的地方, 那么有什么意义呢? 所以最后你这个visited应该用来mark这个path, 而不是一个CC;
这也是以前一直困扰我的一个问题, 就是到底什么样的DFS才需要记得undo/backtrack; 这里算是给了一个答案, 当你需要mark的是一个path的时候, 那么就应该有一个undo操作;
当然这里的这个visited可以用另外一个方案, 就是用ontains之类的操作来完成, 而且**mark path with 思路的另外一个优势在于, 自动不需要undo; 但是这个思路需要你用string, 而不是我上面用的integer来表达一个path, 但是这里不知道为什么有一个bug;
string hash bug
如果用string来表示accum这个path, 那么我们就可以不需要visited; 但是不知道为什么, 我用string来记录path的时候, 最后在set的size计算上面有bug: 1, 2, 3三个的结果都是对的, 但是[1,3]的结果居然不是这三个之和. 我debug的时候发现是3的某些path好像和[1,2]的某些path有collision, 这个具体什么原因我是真不知道, 按理说长度都不一样, 怎么可能会collision; 不过最后干脆换成integer来做, 反正也还快一点;
不过最后这个算法毕竟是TLE了, 也是没有什么办法;
既然问题是超时, 那么我考虑是不是可以用一些技巧来加速一下, 下面这个算法是利用对称性完成的一点加速:
class Solution {
static int[][] increments1 = {
{-1,0}, {1,0}, {0, -1}, {0,1},
{-1, -1}, {-1, 1}, {1, -1}, {1, 1},
};
static int[][] increments2 = {
{-1, -2}, {-1,2},{1,-2},{1,2},
{-2,-1}, {-2,1}, {2, -1}, {2, 1},
};
public int numberOfPatterns(int m, int n) {
int res = 0;
for (int k = m; k <= n; k++) {
res += dfs (1, 1, new HashSet<Integer> (), new boolean[3][3], 0) +
4 * (dfs (0, 0, new HashSet<Integer> (), new boolean[3][3], 0) +
dfs (0, 1, new HashSet<Integer> (), new boolean[3][3], 0));
}
return res;
}
int dfs (int x, int y, Set<Integer> paths, boolean[][] visited, int step, int {
if (!isValidXY(x, y) || visited[x][y])
return 0;
visited[x][y] = true;
10 + (3 * x + y + 1);
step--;
for (int[] incre : increments1) {
dfs (x + incre[0], y + incre[1], paths, visited, step,
if (isValidXY (x + incre[0], y + incre[1]) && visited[x + incre[0]][y + incre[1]])
dfs (x + 2 * incre[0], y + 2 * incre[1], paths, visited, step,
}
for (int[] incre : increments2)
dfs (x + incre[0], y + incre[1], paths, visited, step,
visited[x][y] = false; // subtle but critical
if (step == 0)
paths.add ( //critical position: pre-leaf is better than leaf here
return paths.size ();
}
boolean isValidXY (int x, int y) {
return !(x < 0 || x >= 3 || y < 0 || y >= 3);
}
}
可惜还是不够快;
最后又想到一个方法, 就是不用针对[m, n]里面的每一个数字单独来一次DFS, 而是可以一个DFS里面就collect完. 最后这样得到的算法是上面的算法, 速度是725ms (1%), 不过好歹是AC了;
又稍微优化了一下, 在recursion的过程中维护accum的length, 而不是专门用一个log去计算; 不过并没有得到足够明显的加速;
进一步优化, 把set去掉了: 因为用了visited这个记录, 所以这个算法本身可以保证unique, 所以不需要专门用一个set去count, 直接用一个int就行了; 但是即使是这样, 最后的速度还是500ms多, 还是很慢;
这个是到这个时候位置的版本:
class Solution {
static int[][] increments1 = {
{-1,0}, {1,0}, {0, -1}, {0,1},
{-1, -1}, {-1, 1}, {1, -1}, {1, 1},
};
static int[][] increments2 = {
{-1, -2}, {-1,2},{1,-2},{1,2},
{-2,-1}, {-2,1}, {2, -1}, {2, 1},
};
public int numberOfPatterns(int m, int n) {
int res = 0;
res += dfs (1, 1, new boolean[3][3], 0, m, n, 0, 0) +
4 * (dfs (0, 0, new boolean[3][3], 0, m, n, 0, 0) +
dfs (0, 1, new boolean[3][3], 0, m, n, 0, 0));
return res;
}
int dfs (int x, int y, boolean[][] visited, int count, int m, int n, int int pathLen) {
if (!isValidXY(x, y) || visited[x][y])
return count; // can't return 0 here!
visited[x][y] = true;
10 + (3 * x + y + 1);
pathLen++;
if (m <= pathLen && pathLen <= n)
count++; //critical position: pre-leaf is better than leaf here
for (int[] incre : increments1) {
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
if (isValidXY (x + incre[0], y + incre[1]) && visited[x + incre[0]][y + incre[1]])
count = dfs (x + 2 * incre[0], y + 2 * incre[1], visited, count, m, n, pathLen);
}
for (int[] incre : increments2)
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
visited[x][y] = false; // subtle but critical
return count;
}
boolean isValidXY (int x, int y) {
return !(x < 0 || x >= 3 || y < 0 || y >= 3);
}
}
这里有一个有趣的小技巧, 注意看我count只不过是一个int参数, 但是我最后也用他完成了一个类似global的记录功能; 这个就是因为擅用返回值的缘故, 加上我们的count是只增不减, 所以只要在每一个iteration里面记得勤快的更新count就行了, 最后返回最大值; 自己想想为什么这个逻辑行得通;
又想到一个优化: accum本身并没有需要, 我们只要用pathLen记录他的长度就行了; 最后得到的算法就是上面的算法, 不过速度还是不好, 400+;
这时候的算法:
class Solution {
static int[][] increments1 = {
{-1,0}, {1,0}, {0, -1}, {0,1},
{-1, -1}, {-1, 1}, {1, -1}, {1, 1},
};
static int[][] increments2 = {
{-1, -2}, {-1,2},{1,-2},{1,2},
{-2,-1}, {-2,1}, {2, -1}, {2, 1},
};
public int numberOfPatterns(int m, int n) {
int res = 0;
res += dfs (1, 1, new boolean[3][3], 0, m, n, 0) +
4 * (dfs (0, 0, new boolean[3][3], 0, m, n, 0) +
dfs (0, 1, new boolean[3][3], 0, m, n, 0));
return res;
}
int dfs (int x, int y, boolean[][] visited, int count, int m, int n, int pathLen) {
if (!isValidXY(x, y) || visited[x][y])
return count; // can't return 0 here!
visited[x][y] = true;
pathLen++;
if (m <= pathLen && pathLen <= n)
count++; //critical position: pre-leaf is better than leaf here
for (int[] incre : increments1) {
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
if (isValidXY (x + incre[0], y + incre[1]) && visited[x + incre[0]][y + incre[1]])
count = dfs (x + 2 * incre[0], y + 2 * incre[1], visited, count, m, n, pathLen);
}
for (int[] incre : increments2)
count = dfs (x + incre[0], y + incre[1], visited, count, m, n, pathLen);
visited[x][y] = false; // subtle but critical
return count;
}
boolean isValidXY (int x, int y) {
return !(x < 0 || x >= 3 || y < 0 || y >= 3);
}
}
在优化思考的时候, 我看到一个问题, 这个题目虽然我意识到了undo, 但是我的undo的方法跟discussion和editorial他们的写法也不太一样, 他们都是在pre-node的位置进行do and undo, 而我是在node本身的body里面进行这个操作的; 感觉我这个操作位置相对来说比他们的方法更加麻烦一些;
另外, 看完了editorial和discussion之后, 我本来以为我的算法更加general一些, 应该可以直接拓展到N比3更大的情形, 不过后来发现一个问题, 并不能, 因为当N更大的board的时候, 你的increments2就需要修改, 会大很多, 而且DFS里面第一个循环的jump判断也更复杂, 不是一个二倍就能完成的;
但是我尝试了一个简单的扩展, 就是不修改increments2和其他逻辑, 只修改N, 结果发现, N的修改对于最后的结果没有影响? 这个能拓展成什么题目? increments2的那些move其实叫做knight move, 然后increments1我用来记录是一步和两步的move. 这个题目设定好像还没有专门见到过, 不过长个心眼还是可以的, 我的算法可以解决任意N的情况下的这个题目;
editorial
public class Solution {
private boolean used[] = new boolean[9];
public int numberOfPatterns(int m, int n) {
int res = 0;
for (int len = m; len <= n; len++) {
res += calcPatterns(-1, len);
for (int i = 0; i < 9; i++) {
used[i] = false;
}
}
return res;
}
private boolean isValid(int index, int last) {
if (used[index])
return false;
// first digit of the pattern
if (last == -1)
return true;
// knight moves or adjacent cells (in a row or in a column)
if ((index + last) % 2 == 1)
return true;
// indexes are at both end of the diagonals for example 0,0, and 8,8
int mid = (index + last)/2;
if (mid == 4)
return used[mid];
// adjacent cells on diagonal - for example 0,0 and 1,0 or 2,0 and //1,1
if ((index%3 != last%3) && (index/3 != last/3)) {
return true;
}
// all other cells which are not adjacent
return used[mid];
}
private int calcPatterns(int last, int len) {
if (len == 0)
return 1;
int sum = 0;
for (int i = 0; i < 9; i++) {
if (isValid(i, last)) {
used[i] = true;
sum += calcPatterns(i, len - 1);
used[i] = false;
}
}
return sum;
}
}
这个算法还算可以, 至少速度是可以接受的; 他注意到了这里这个distinct的条件, 所以立刻想到用used来做一个backtracking的算法; 注意看他calcPatterns返回值的设计: 只在leaf的位置返回1, 所以最后是一个标准的dfs count的思路;
这个算法除去上面讨论的这些, 剩下的复杂度基本就在于isValid这个函数上面了; 分析他的这个算法, 可以看到在这种DFS path问题上的一个小结: 当我们有这种需要DFS path的需求的时候:
- 一种思路就是我自己最熟悉的, pick next move, 这个move我一般用increment来完成;
- 另外一种思路就是这里第一次见到, 直接pick next position, 也就是直接pick move的终点, 而不是move的方向; 这种思路在这里就非常的有效; 更进一步, 一般当board比较小的时候, 用这种方法往往比一步一步的pick direction更加方便;
- 用这种思路的一个必然要解决的问题是, 怎样validate next position; 这里给出了一个思路, 不过一般真正用到这种思路的时候, validate都是通过一个类似枚举的思路完成的;
discussion最优解, 好像速度也很快:
@david.liu said in Simple and concise Java solution in 69ms:
The general idea is DFS all the possible combinations from 1 to 9 and skip invalid moves along the way.
We can check invalid moves by using a jumping table. e.g. If a move requires a jump and the key that it is crossing is not visited, then the move is invalid. Furthermore, we can utilize symmetry to reduce runtime, in this case it reduced from ~120ms to ~70ms.
I felt clueless when first encountered this problem, and considered there must be lots of edge cases. Turns out, it's pretty straight forward. Hope this solution helps :D
private int[][] jumps;
private boolean[] visited;
public int numberOfPatterns(int m, int n) {
jumps = new int[10][10];
jumps[1][3] = jumps[3][1] = 2;
jumps[4][6] = jumps[6][4] = 5;
jumps[7][9] = jumps[9][7] = 8;
jumps[1][7] = jumps[7][1] = 4;
jumps[2][8] = jumps[8][2] = 5;
jumps[3][9] = jumps[9][3] = 6;
jumps[1][9] = jumps[9][1] = jumps[3][7] = jumps[7][3] = 5;
visited = new boolean[10];
int count = 0;
count += DFS(1, 1, 0, m, n) * 4; // 1, 3, 7, 9 are symmetrical
count += DFS(2, 1, 0, m, n) * 4; // 2, 4, 6, 8 are symmetrical
count += DFS(5, 1, 0, m, n);
return count;
}
private int DFS(int num, int len, int count, int m, int n) {
if (len >= m) count++; // only count if moves are larger than m
len++;
if (len > n) return count;
visited[num] = true;
for (int next = 1; next <= 9; next++) {
int jump = jumps[num][next];
if (!visited[next] && (jump == 0 || visited[jump])) {
count = DFS(next, len, count, m, n);
}
}
visited[num] = false; // backtracking
return count;
}
实际上这个算法的枚举的部分比editorial那个算法还要严重; 我感觉这个题目就是你枚举的部分越多, 算法越不general, 最后的速度越好. 我认为
这个是1pass优化:
public int numberOfPatterns(int m, int n) {
int[][] skip = new int[10][10];
skip[1][3] = skip[3][1] = 2;
skip[1][7] = skip[7][1] = 4;
skip[3][9] = skip[9][3] = 6;
skip[7][9] = skip[9][7] = 8;
skip[1][9] = skip[9][1] = skip[2][8] = skip[8][2] = skip[3][7] = skip[7][3] = skip[4][6] = skip[6][4] = 5;
boolean[] vis = new boolean[10];
int ret = dfs(1, 0, m, n, 0, skip, vis) * 4;
ret += dfs(2, 0, m, n, 0, skip, vis) * 4;
ret += dfs(5, 0, m, n, 0, skip, vis);
return ret;
}
private int dfs(int cur, int l, int m, int n, int ret, int[][] skip, boolean[] vis) {
l++;
if (l >= m) ret++;
if (l == n) return ret;
vis[cur] = true;
for (int next = 1; next <= 9; next++) {
if (!vis[next] && (skip[cur][next] == 0 || vis[skip[cur][next]])) {
ret = dfs(next, l + 1, m, n, ret, skip, vis);
}
}
vis[cur] = false;
return ret;
}
submission最优解, 跟上面discussion看到的大部分解法差不多:
class Solution {
public int numberOfPatterns(int m, int n) {
boolean[] visited = new boolean[10];
visited[0] = true;
int[][] jumps = new int[10][10];
jumps[1][3] = jumps[3][1] = 2;
jumps[1][7] = jumps[7][1] = 4;
jumps[7][9] = jumps[9][7] = 8;
jumps[9][3] = jumps[3][9] = 6;
jumps[4][6] = jumps[6][4] = jumps[2][8] = jumps[8][2] = jumps[1][9] = jumps[9][1] = jumps[3][7] = jumps[7][3] = 5;
int count = 0;
count += 4 * dfs(1, 1, 0, m, n, visited, jumps);
count += 4 * dfs(2, 1, 0, m, n, visited, jumps);
count += dfs(5, 1, 0, m, n, visited, jumps);
return count;
}
private int dfs(int num, int len, int count, int m, int n, boolean[] visited, int[][] jumps) {
if (len >= m) count++;
len++;
if (len > n) return count;
visited[num] = true;
for (int next = 1; next <= 9; next++) {
if (!visited[next] && (jumps[num][next] == 0 || visited[jumps[num][next]])) {
count = dfs(next, len, count, m, n, visited, jumps);
}
}
visited[num] = false;
return count;
}
}
Problem Description
Given an Android 3x3 key lock screen and two integers m and n, where 1 ≤ m ≤ n ≤ 9, count the total number of unlock patterns of the Android lock screen, which consist of minimum of m keys and maximum n keys.
Rules for a valid pattern:
- Each pattern must connect at least m keys and at most n keys.
- All the keys must be distinct.
- If the line connecting two consecutive keys in the pattern passes through any other keys, the other keys must have previously selected in the pattern. No jumps through non selected key is allowed.
- The order of keys used matters.
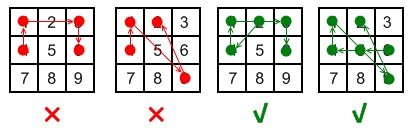
Explanation:
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
Invalid move: 4 - 1 - 3 - 6
- Line 1 - 3 passes through key 2 which had not been selected in the pattern.
Invalid move: 4 - 1 - 9 - 2
- Line 1 - 9 passes through key 5 which had not been selected in the pattern.
Valid move: 2 - 4 - 1 - 3 - 6
- Line 1 - 3 is valid because it passes through key 2, which had been selected in the pattern
Valid move: 6 - 5 - 4 - 1 - 9 - 2
- Line 1 - 9 is valid because it passes through key 5, which had been selected in the pattern.
Example:
- Given m = 1, n = 1, return 9.
Credits:
- Special thanks to @elmirap for adding this problem and creating all test cases.
Difficulty:Medium
Total Accepted:18.3K
Total Submissions:41K
Contributor:LeetCode
Companies
google
Related Topics
dynamic programmingbacktracking